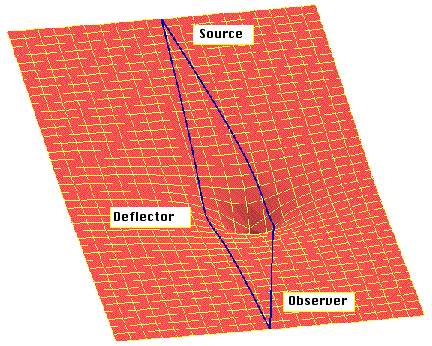
In a system where lensing occurs there is a
In general relativity, the presence of matter (energy density) can curve spacetime, and the path of a light ray will be deflected as a result. This process is called gravitational lensing and in many cases can be described in analogy to the deflection of light by (e.g. glass) lenses in optics. Many useful results for cosmology have come out of using this property of matter and light.
For many of the cases of interest one does not need to fully solve the general relativistic equations of motion for the coupled spacetime and matter, because the bending of spacetime by matter is small. (Quantitatively the matter bending space is moving slowly relative to c, the speed of light and the "gravitational potential" Phi induced by the matter obeys |Phi|/c2 << 1 .)
A sketch of the paradigm of a lensed system is below
(
source):

In a system where lensing occurs there is a
Strong Lensing
The most extreme bending of light is when the lens is very massive
and the source is close enough to it: in this case light can
take different paths to the observer and more than
one image of the source will appear.
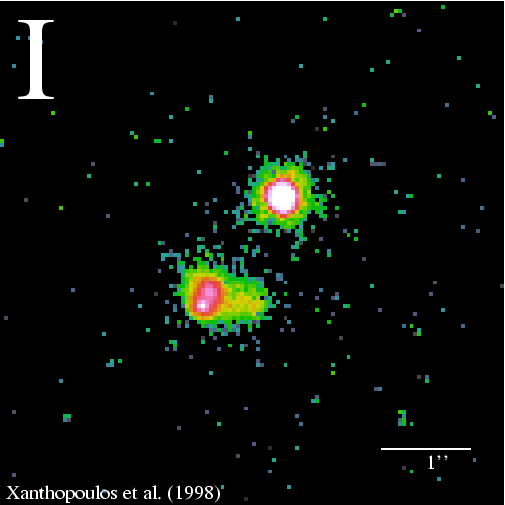 A multiple
image is shown at right
(source).
The first example of a double
image was found in 1979, of a quasar.
The number of lenses discovered
has been used to estimate the volume of space
back to the sources. This volume
depends strongly on cosmological parameters,
in particular the cosmological constant
(a classic reference is
here).
A multiple
image is shown at right
(source).
The first example of a double
image was found in 1979, of a quasar.
The number of lenses discovered
has been used to estimate the volume of space
back to the sources. This volume
depends strongly on cosmological parameters,
in particular the cosmological constant
(a classic reference is
here).
If the source varies with time, the multiple
images will vary with time as well.
However, the light doesn't travel the same distance to each image,
due to the bending of space. So there will be time delays for
the changes in the images. These time delays can be used to
calculate the hubble constant
H0.
A few systems with these time delays have been
found and are under study. Much of the subtlety in this work
lies with constructing the model of the mass distribution
forming the lens
(see this
review for
technical detail).
In some special cases the alignment of the source and the lens will be
such that light will be deflected to the observer in
an "Einstein ring." Some examples and references can
be found here on
Wikipedia.
More often than a ring, the source may get stretched out and curved,
and form a tangential or radial arc. A lot of mass is needed to
cause an arc to appear, so that properties of arcs (numbers, size,
geometry) can often be used
to study massive objects like
clusters.
One can also, given a set of images, try to reconstruct the lens
mass distribution (for an example of reconstructing a cluster as a lens
see this
technical paper).
Weak Lensing
In many cases the lens is not strong enough to form multiple images or
arcs. However, the source can still be distorted: both stretched (shear)
and magnified (convergence). If all sources were well known in
size and shape, one could just use the shear and convergence to
deduce the properties of the lens. However, usually one does not know
the intrinsic properties of the sources, but has information about
the average properties. The statistics of the sources can then be used to
get information about the lens. For instance, galaxies in general
aren't perfectly spherical, but if one has a collection of galaxies
one doesn't expect them all to be lined up.
Thus, if this set of galaxies is lensed, on average, or statistically,
there will be some overall shear and/or convergence imposed on the
distribution, which will give information about the intervening lens(es).
There is a distribution of galaxies far enough away that can be
treated as sources, and thus
clusters nearby can be "weighed" (i.e. have their mass measured)
using their lensing. Superclusters have been considered as well.
In addition, theories of cosmology predict the
distribution of
large
scale structure, the distribution of matter in the universe.
The statistical properties of the large scale
structure (e.g. the probability of finding a galaxy at one place
when there is another a certain distance away) can also be measured by
weak lensing, because the matter will produce shear and convergence
in distant sources (which can be galaxies, or
the
cosmic
microwave background, for example).
Weak lensing is a useful complement to measures of the distribution of
luminous mass such as
galaxy surveys. Lensing measures all the mass, in particular
the
dark matter as well as the luminous matter.
Microlensing
There are ongoing searches to use lensing to find a type of
dark matter called MACHOs (massive compact halo objects). Although
MACHOs,
as dark matter, cannot be seen themselves, if they pass in front of a
source (e.g. a star nearby), they can cause
the star to become brighter for a while, e.g. days or weeks.
This effect has been observed,
but determinations of
the dark matter are not yet conclusive.
Observations are underway by many groups.
See these notes by Michael Richmond on Gravitational Microlensing: Searches
and Results.
Some web references:
Back to
What is Theoretical Cosmology?
comments to jcohn@berkeley.edu
In some cases the lensing is of an image that is
so small or faint that one doesn't see the multiple images--
the additional light bent towards the observer just means that the source
appears brighter. (The surface brightness remains unchanged but as
more images of the object appear the object
appears bigger and hence brighter.) This lensing can have effects in
many measurements, as sources which would have otherwise been too dim
become visible. This can be helpful, as when one wants
to view objects that would otherwise be too far away.
It can also be a problem, for example
when one is trying to measure all objects brighter
than a certain amount in a certain region and lensing introduces objects
by magnifying objects enough to bring them into the sample.
(See also the review at Wikipedia.)
last updated Dec. 13, 2010.