Baryon acoustic oscillations and dark energy
There are now several independent ways to show that the expansion of the
Universe is accelerating.
This indicates that:
- Our theory of gravity is wrong, or
- The universe is dominated by a material which violates the strong
energy condition.
If (2) then it cannot be any classical fluid, but some weird quantum stuff
which dominates the energy density of the Universe (today).
We refer to it as dark energy.
We see the dark energy through its effects on the expansion rate of
the Universe. Indeed dark energy was first found by measurements of
cosmic expansion, although models containing it had been around for
several years.
To constrain the nature of dark energy we need to be able to
measure the expansion rate of the Universe and there
are three main approaches:
- Standard candles: which measure the luminosity distance as
a function of redshift.
- Standard rulers: which measure the angular diameter distance
and expansion rate as a function of redshift.
- Growth of fluctuations.
Both the angular diameter and luminosity distances are integrals of
the (inverse) expansion rate and thus encode the effects of dark energy.
Consider (2) further.
Suppose we had an object whose length (e.g. in meters) we knew as a function
of cosmic epoch. By measuring the angle subtended by this ruler as a function
of redshift we map out the angular diameter distance, d(z). By measuring the
redshift interval associated with this distance we map out the Hubble
parameter, H(z).
To get competitive constraints on dark energy we need to be able to see
changes in H(z) at the 1% level -- this would give us statistical errors
in the DE equation of state of O(10%).
- We need to be able to calibrate the ruler accurately over most of
the age of the universe.
- We need to be able to measure the ruler over much of the volume of
the universe.
- We need to be able to make ultra-precise measurements of the ruler.
Cosmological objects can probably never be uniform enough so we
use statistics of the large-scale distribution of matter and radiation.
If we work on large scales or early times perturbative treatment is valid
and calculations under control.
Preferred length scales arising from physics of the early universe are
imprinted on the distribution of mass and radiation and form time-independent
rulers.
Let us consider the early universe, which was composed of a coupled plasma
of energetic photons and ionized hydrogen (protons and electrons) plus other
trace elements and the mysterious dark matter.
Start with a single perturbation.
The plasma is totally uniform except for an excess of matter at the origin.
High pressure drives the gas+photon fluid outward at speeds approaching the
speed of light. In the panels below we show some snapshots from this
process, with the baryon density shown in the left panel, the photon
density in the right panel and the mass profile as a graph in the final
panel.
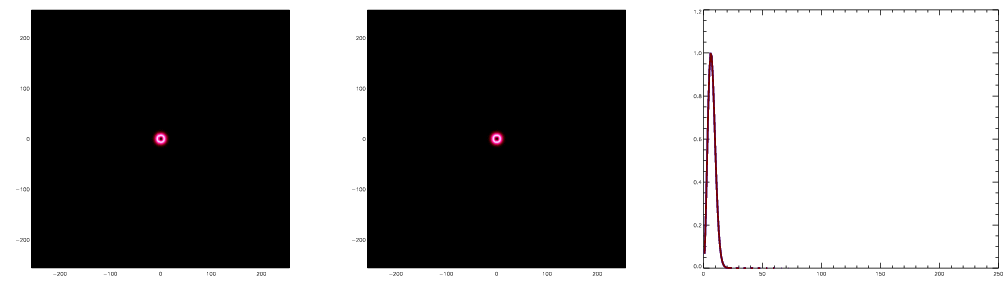 Initially both the photons and the baryons move outward together, the radius of the shell moving at over half the speed of light
Initially both the photons and the baryons move outward together, the radius of the shell moving at over half the speed of light
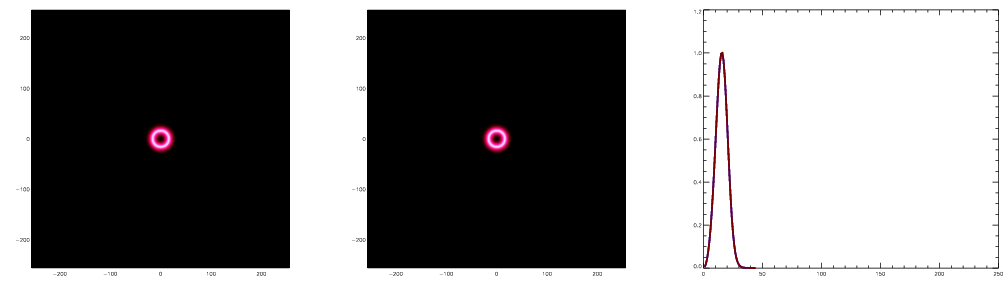 This expansion continues for 105 years
This expansion continues for 105 years
 After 105 years the universe has cooled enough the protons
capture the electrons to form neutral Hydrogen.
This decouples the photons from the baryons.
The former quickly stream away, leaving the baryon peak stalled.
After 105 years the universe has cooled enough the protons
capture the electrons to form neutral Hydrogen.
This decouples the photons from the baryons.
The former quickly stream away, leaving the baryon peak stalled.
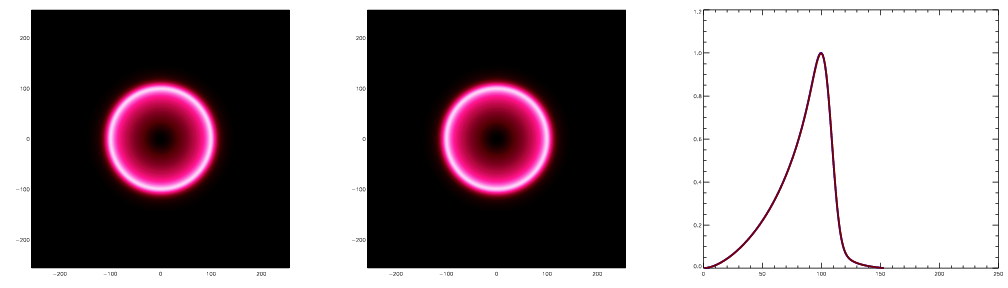
 The photons continue to stream away while the baryons, having lost their
motive pressure, remain in place.
The photons continue to stream away while the baryons, having lost their
motive pressure, remain in place.
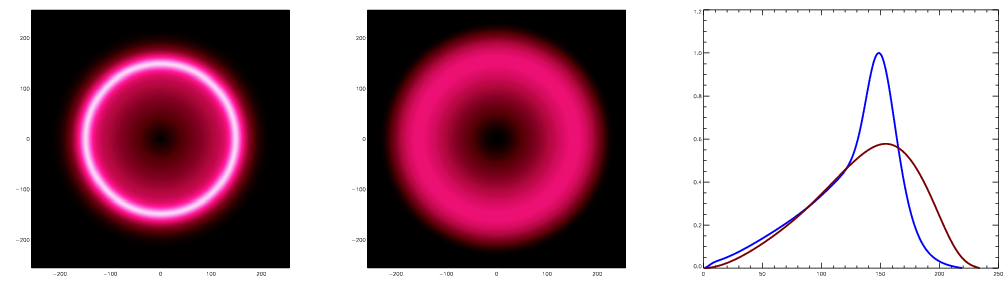
 The photons have become almost completely uniform, but the baryons remain
overdense in a shell 100Mpc in radius. In addition, the large gravitational
potential well which we started with starts to draw material back into it.
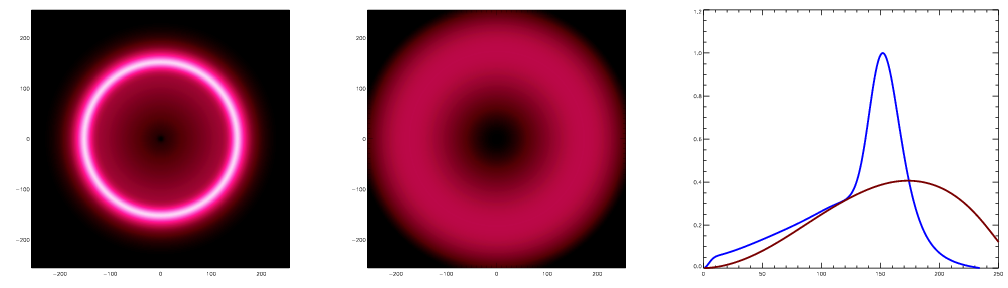
The photons have become almost completely uniform, but the baryons remain
overdense in a shell 100Mpc in radius. In addition, the large gravitational
potential well which we started with starts to draw material back into it.
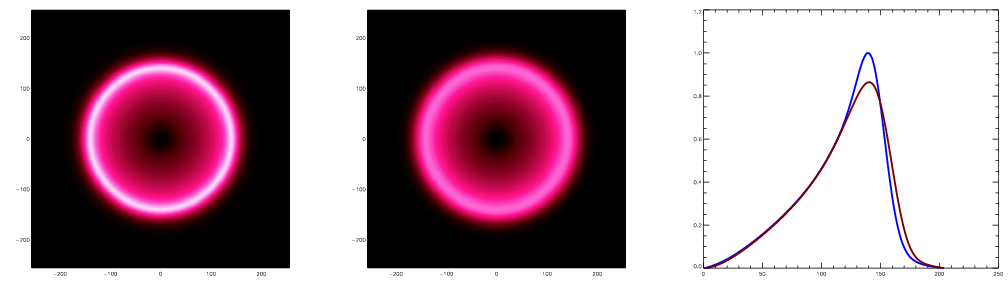
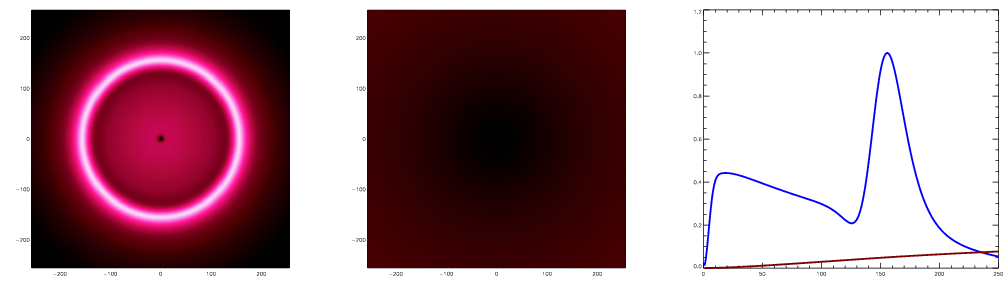 As the perturbation grows by O(1000) the baryons and DM reach equilibrium
densities in the ratio Wb/Wm. The final configuration is our original peak
at the center (which we put in by hand) and an echo in a shell roughly
100Mpc in radius. The radius of this shell is known as the sound horizon.
As the perturbation grows by O(1000) the baryons and DM reach equilibrium
densities in the ratio Wb/Wm. The final configuration is our original peak
at the center (which we put in by hand) and an echo in a shell roughly
100Mpc in radius. The radius of this shell is known as the sound horizon.
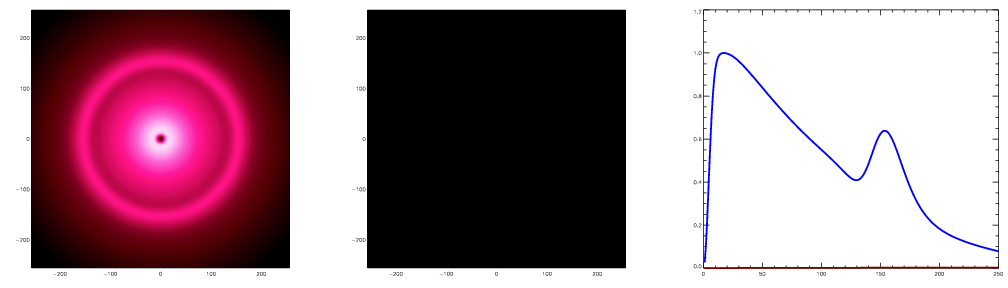
Features of baryon oscillations:
- Firm prediction of models with baryons
- Positions well predicted once (physical) matter and baryon density
known - calibrated by the CMB.
- Oscillations are sharp, unlike other features of the power spectrum.
- Internal cross-check: d should be the integral of H(z).
- Since have d(z) for several zs can check spatial flatness:
d(z1+z2) = d(z1)+d(z2)+O(curvature)
- Ties low-z distance measures (e.g. SNe) to absolute scale defined by
the CMB.
Thus the BAO program is (in principle) straightforward. One finds a
tracer of the mass density field (e.g. galaxies or the
Ly-a forest)
and computes its 2-point function. The features in the 2-point function
correspond to the sound horizon, roughly 100Mpc in size. By knowing the
angle (and redshift interval) this distance subtends one measures d(z).
Comparing to the value at z~103 allows us to constrain the
evolution of the dark energy.
The problem is that the ruler we are using is inconveniently large. It
is only with the latest generation of large galaxy redshift surveys that
we are able to probe the giga-parsec volumes required to make a precision
measurement of the BAO signal.
In order to turn this idea into a workable measurement there are number
of higher order effects which need to be taken into account. These involve
the details of how the statistics are measured on the galaxy redshift
survey and the corrections for non-linearity, galaxy bias and redshift space
distortions. You can find more details on these technical aspect by
following the links below.
For further, more technical, information see these
Lectures given
at the 2007 Santa Fe cosmology workshop or the 2008
IUCCA school.
or these
Lectures
from the 2010 Santa Fe cosmology workshop.
 Initially both the photons and the baryons move outward together, the radius of the shell moving at over half the speed of light
Initially both the photons and the baryons move outward together, the radius of the shell moving at over half the speed of light
 This expansion continues for 105 years
This expansion continues for 105 years
 After 105 years the universe has cooled enough the protons
capture the electrons to form neutral Hydrogen.
This decouples the photons from the baryons.
The former quickly stream away, leaving the baryon peak stalled.
After 105 years the universe has cooled enough the protons
capture the electrons to form neutral Hydrogen.
This decouples the photons from the baryons.
The former quickly stream away, leaving the baryon peak stalled.
 The photons continue to stream away while the baryons, having lost their
motive pressure, remain in place.
The photons continue to stream away while the baryons, having lost their
motive pressure, remain in place.

 The photons have become almost completely uniform, but the baryons remain
overdense in a shell 100Mpc in radius. In addition, the large gravitational
potential well which we started with starts to draw material back into it.
The photons have become almost completely uniform, but the baryons remain
overdense in a shell 100Mpc in radius. In addition, the large gravitational
potential well which we started with starts to draw material back into it.
 As the perturbation grows by O(1000) the baryons and DM reach equilibrium
densities in the ratio Wb/Wm. The final configuration is our original peak
at the center (which we put in by hand) and an echo in a shell roughly
100Mpc in radius. The radius of this shell is known as the sound horizon.
As the perturbation grows by O(1000) the baryons and DM reach equilibrium
densities in the ratio Wb/Wm. The final configuration is our original peak
at the center (which we put in by hand) and an echo in a shell roughly
100Mpc in radius. The radius of this shell is known as the sound horizon.
