The Thomson scattering cross section depends on polarization as (see e.g. [Chandrasekhar] 1960)
![]()
where ![]() (
( ![]() ) are the incident (scattered)
polarization directions. Heuristically, the incident light sets up
oscillations of the target electron in the direction of the electric
field vector
) are the incident (scattered)
polarization directions. Heuristically, the incident light sets up
oscillations of the target electron in the direction of the electric
field vector ![]() , i.e. the polarization.
The scattered radiation intensity thus peaks in the direction normal to,
with polarization parallel to, the incident polarization.
More formally, the polarization dependence of the cross section is
dictated by electromagnetic gauge invariance and thus follows from very
basic principles of fundamental physics.
, i.e. the polarization.
The scattered radiation intensity thus peaks in the direction normal to,
with polarization parallel to, the incident polarization.
More formally, the polarization dependence of the cross section is
dictated by electromagnetic gauge invariance and thus follows from very
basic principles of fundamental physics.
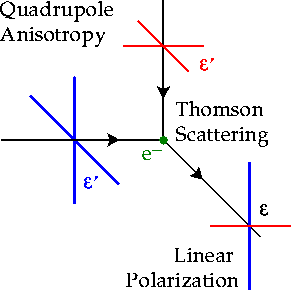
If the incoming radiation field were isotropic, orthogonal polarization
states from incident directions separated by ![]() would balance so
that the outgoing radiation would remain unpolarized. Conversely,
if the incident radiation field possesses a quadrupolar variation
in intensity or temperature (which possess intensity peaks at
would balance so
that the outgoing radiation would remain unpolarized. Conversely,
if the incident radiation field possesses a quadrupolar variation
in intensity or temperature (which possess intensity peaks at ![]() separations), the result is a linear polarization of the scattered
radiation (see Fig. 1).
A reversal in sign of the temperature fluctuation corresponds to a
separations), the result is a linear polarization of the scattered
radiation (see Fig. 1).
A reversal in sign of the temperature fluctuation corresponds to a
![]() rotation of the polarization, which reflects the spin-2
nature of polarization.
rotation of the polarization, which reflects the spin-2
nature of polarization.
In terms of a multipole decomposition of the radiation field into spherical
harmonics, ![]() , the five quadrupole moments are
represented by
, the five quadrupole moments are
represented by ![]() ,
, ![]() .
The orthogonality of the spherical harmonics guarantees that no other moment
can generate polarization from Thomson scattering.
In these spherical coordinates, with the north pole at
.
The orthogonality of the spherical harmonics guarantees that no other moment
can generate polarization from Thomson scattering.
In these spherical coordinates, with the north pole at ![]() , we call
a N-S (E-W) polarization component Q>0 (Q<0) and a NE-SW (NW-SE) component
U>0 (U<0).
The polarization amplitude and angle clockwise from north are
, we call
a N-S (E-W) polarization component Q>0 (Q<0) and a NE-SW (NW-SE) component
U>0 (U<0).
The polarization amplitude and angle clockwise from north are
![]()
Alternatively, the Stokes parameters Q and U represent the diagonal and
off diagonal components of the symmetric, traceless, ![]() intensity
matrix
in
the polarization plane spanned by (
intensity
matrix
in
the polarization plane spanned by ( ![]() ,
, ![]() ),
),
![]()
where ![]() are the Pauli matrices and circular polarization
is assumed absent.
are the Pauli matrices and circular polarization
is assumed absent.
If Thomson scattering is rapid, then the randomization of photon directions that results destroys any quadrupole anisotropy and polarization. The problem of understanding the polarization pattern of the CMB thus reduces to understanding the quadrupolar temperature fluctuations at last scattering.
Temperature perturbations have 3 geometrically distinct sources:
the scalar (compressional), vector (vortical) and tensor (gravitational wave)
perturbations.
Formally, they form the irreducible basis of the symmetric metric tensor.
We shall consider each of these below and show that the
scalar, vector, and tensor quadrupole anisotropy correspond to
![]() respectively.
This leads to different patterns of polarization for the
three sources as we shall discuss in §3.
respectively.
This leads to different patterns of polarization for the
three sources as we shall discuss in §3.