Any polarization pattern on the sky can be separated into ``electric'' (E)
and ``magnetic'' (B) components
.
This decomposition is useful both observationally and theoretically, as we
will discuss below.
There are two equivalent ways of viewing the modes that reflect their global
and local properties respectively.
The nomenclature reflects the global property. Like multipole radiation,
the harmonics of an E-mode have 
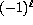parity on the sphere, whereas
those of a B-mode have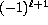 
parity.
Under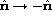 
, the E-mode thus remains unchanged
for even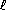 
, whereas the B-mode changes sign as illustrated for the
simplest case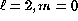 
in Fig. 9
(recall that a rotation by 90 
represents a change in sign).
Note that the E and B multipole patterns are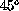 
rotations of each
other, i.e.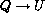 
and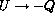 
.
Since this parity property is obviously rotationally invariant, it will
survive integration over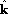 
.
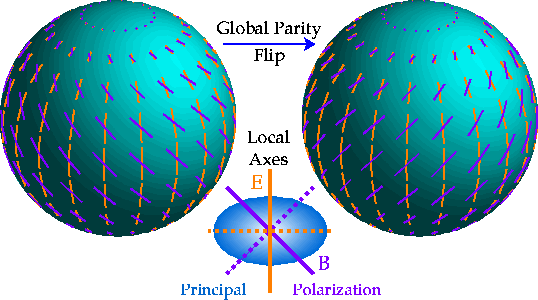
The local view of E and B-modes involves the second derivatives
of the polarization amplitude (second derivatives because
polarization is a tensor or spin-2 object).
In much the same way that the distinction between electric and magnetic
fields in electromagnetism involves vanishing of gradients or curls
(i.e. first derivatives) for the polarization there are conditions on the
second (covariant) derivatives of Q and U.
For an E-mode, the difference in second (covariant) derivatives of U
along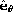 
and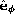 
vanishes as does that for Q
along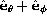 
and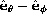 
.
For a B-mode, Q and U are interchanged. Recalling that a Q-field
points in the 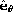or 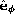direction and a U-field
in the crossed direction, we see that the Hessian or curvature matrix of
the polarization amplitude has principle axes in the same sense as the
polarization for E and 45 crossed with it for B
(see Fig. 9).
Stated another way, near a maximum of the polarization (where the first
derivative vanishes) the direction of greatest change in the polarization
is parallel/perpendicular and at 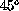degrees to the polarization in
the two cases.
The distinction is best illustrated with examples. Take the simplest case
of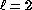 
, m=0 where the E-mode is a 
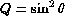field and the
B-mode is a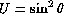 
field (see Fig. 4).
In both cases, the major axis of the curvature lies in the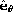
direction. For the E-mode, this is in the same sense; for the B-mode it
is crossed with the polarization direction. The same holds true for the
m=1,2 modes as can be seen by inspection of Fig. 6 and
8.
