From a broad perspective, the main impact of CMB anisotropies has been to shrink substantially the range of cosmological models under active discussion. This is not always easy to see, since the number of models proposed at any time seems to be determined more by the number of theorists working in the field than by any constraints provided by the data. Moreover, it sometimes seems that no class of model has been ruled out. However, looking back a decade in the literature makes it clear that this is not true.
Even before COBE, the high level of isotropy of the CMB was perhaps the best possible evidence that the large-scale properties of the Universe were well described by the Friedman-Robertson-Walker metric. The assumption of homogeneity and isotropy, initially made for purely aesthetic reasons, turned out to be an extremely good approximation to the real Universe. As the limits on anisotropy became stronger and stronger, the number of models based on anything but the FRW metric became fewer and fewer.
Currently popular models assume that the matter in the FRW Universe is composed mostly of Cold Dark Matter (CDM), with smaller admixtures of baryons and perhaps massive neutrinos, plus curvature and/or vacuum components. For these CDM-inspired models, the CMB data have been instrumental in narrowing the range of possibilities, and most popular flavours of CDM now give remarkably similar predictions. Models dominated by Hot Dark Matter, already in trouble before COBE, are no longer discussed. Two other classes of models, namely defects and isocurvature models, have not been ruled out definitively, but they are now very much on the defensive against the weight of data. Explosion models ([Ostriker & Cowie 1981, Ikeuchi 1981, Carr & Ikeuchi 1985, Vishniac, Ostriker & Bertschinger 1985, Wandel 1985, Ostriker & Strassler 1989, Weinberg, Dekel & Ostriker 1989]), super-conducting cosmic string models ([Ostriker, Thompson & Witten 1986, Ostriker & Thompson 1987, Borden, Ostriker & Weinberg 1989]), and late-time phase transition models ([Wasserman 1986, Hill , Schramm & Fry 1989, Press, Ryden & Spergel 1990, Fuller & Schramm 1992, Frieman, Hill & Watkins 1992, Jaffe, Stebbins & Frieman 1994]) have essentially vanished.
Figure 1 shows the current state of CMB measurements.
Included are all detections we are aware of that have been published or
submitted for publication in 1998. The results have been averaged in 12 bins,
equally spaced in ![]() for clarity, and
we have omitted the upper limits on smaller angular scales, most of which
are off the right of the plot with our chosen
for clarity, and
we have omitted the upper limits on smaller angular scales, most of which
are off the right of the plot with our chosen ![]() -axis range. This
figure is meant to be indicative only. More statistically rigorous approaches
exist for combining data sets (e.g. [Bond, Jaffe & Knox 1998]), and such methods should
certainly be used for determining precise constraints on models.
However, Fig. 1 gives
approximately the correct visual impression for the combined constraining power
of today's data.
-axis range. This
figure is meant to be indicative only. More statistically rigorous approaches
exist for combining data sets (e.g. [Bond, Jaffe & Knox 1998]), and such methods should
certainly be used for determining precise constraints on models.
However, Fig. 1 gives
approximately the correct visual impression for the combined constraining power
of today's data.
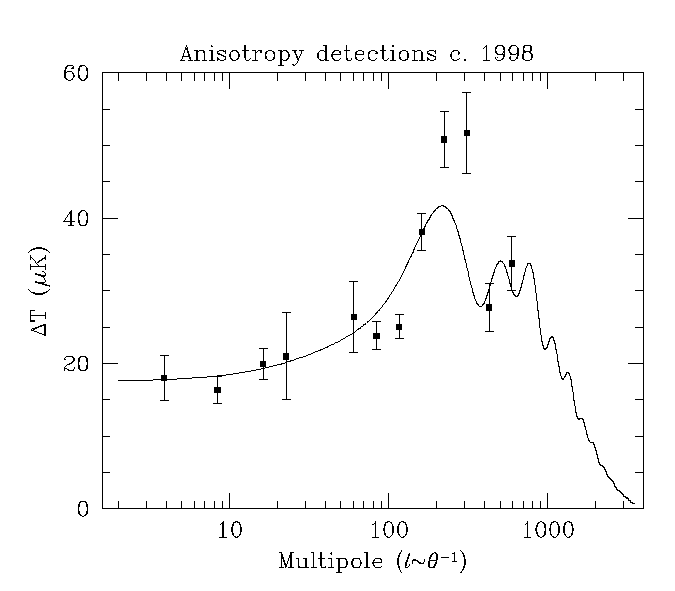 FIG.1:
The current CMB anisotropy detections, averaged in 12 bins equally
spaced in
FIG.1:
The current CMB anisotropy detections, averaged in 12 bins equally
spaced in ![]() (with some bins missing, where no experimental window functions peak).
The y-axis measures the rms fluctuation averaged over the range of angular
scales within the bin, the x-axis is the multipole number
(with some bins missing, where no experimental window functions peak).
The y-axis measures the rms fluctuation averaged over the range of angular
scales within the bin, the x-axis is the multipole number
![]() or 1/theta, with 1 degree near
or 1/theta, with 1 degree near
![]() of 100.
The solid line is the prediction of the `standard' cold dark matter model,
and is included only as an example. We note that creating plots like this
is cosmetology rather than cosmology; such binned data are qualitatively
useful, but should not be used for statistical purposes.
of 100.
The solid line is the prediction of the `standard' cold dark matter model,
and is included only as an example. We note that creating plots like this
is cosmetology rather than cosmology; such binned data are qualitatively
useful, but should not be used for statistical purposes.
Below we list two sets of statements that we believe are supported by the data: the first set contains `fundamental truths' about the Universe; and the second contains statements that will be fundamental truths if confirmed, but that for the present must be regarded more tentatively.
Here is the `A' list:
And the `B' list:
We now discuss these in turn, distinguishing between those demonstrated by COBE alone, and those demonstrated by the measurements at smaller angular scales that have been made since COBE.
2.A.1 Gravitational instability
Perhaps the most useful result of the COBE anisotropy data is the normalization of models of structure formation at large-angles, where the fluctuations in the matter and photons are expected to be in the linear regime. In today's favoured models of structure formation these large-angle anisotropies directly measure the amplitude of the gravitational potential on very large scales, allowing a theoretically clean and precise normalization of the matter power spectrum. This normalization, it turns out (e.g. [Bond, Efstathiou & White 1992]), is in the right ball-park to explain the amplitude of galaxy clustering (and with a little tuning of this or that parameter it is easy to get complete consistency). This is a vindication of our ideas that galaxies grew gradually under the action of gravitational instability.
Before the COBE anisotropy was announced it was often claimed (e.g. [Kolb & Turner 1990]) that extra physics would be needed if the results turned out to yield yet more upper limits; right up to the DMR announcement it was also commonly perceived that inflationary adiabatic models had difficulty having a high enough amplitude to form structure without violating CMB limits (e.g. [Gooding et al. 1993]). The fact that the anisotropies were measured at the levels predicted, in models with cold dark matter and adiabatic fluctuations, showed that there is no need to invoke extra magical processes to form structure by the present day. However, since the photons prevent baryonic matter from collapsing before recombination, we infer that the gravitational potentials had to be dominated by matter which was not prevented from collapsing by photon pressure, i.e. matter that was not coupled to photons and was `dark'. The realization, from studies of the galaxy distribution in the local Universe, that matter formed `bottom up' rather than `top down' constrains the velocity dispersion of the dominant dark matter component to be extremely small - the dark matter must be mostly cold.
2.A.2 Recombination
Here we are moving beyond simply an interpretation of the COBE data, and looking at the large number of detections of anisotropy at degree and sub-degree scales (see Fig. 1). Early reionization of the Universe gives increased optical depth to Thomson scattering from the present back to the epoch of reionization. The extreme case is a universe which did not (re)combine at all and remained ionized for all time. Multiple scattering erases existing anisotropies on scales smaller the horizon. Thus reionization leads to damping of primordial anisotropies on small scales ([Sugiyama, Silk & Vittorio 1993, Hu & White 1997]).
The presence of fluctuations at ![]() is clear evidence that the
Universe was not reionized at a very early epoch. We can be confident that the
Universe recombined at
is clear evidence that the
Universe was not reionized at a very early epoch. We can be confident that the
Universe recombined at ![]() , then remained largely neutral until some
redshift
, then remained largely neutral until some
redshift ![]() , after which it was largely ionized (as implied by
the absence of Gunn-Peterson absorption in the spectra of high-z quasars).
The precise value of
, after which it was largely ionized (as implied by
the absence of Gunn-Peterson absorption in the spectra of high-z quasars).
The precise value of ![]() derived from fits to the data
depends on the cosmological model, but is typically
derived from fits to the data
depends on the cosmological model, but is typically
![]() ([Scott, Silk & White 1995, Tegmark 1998]).
([Scott, Silk & White 1995, Tegmark 1998]).
2.A.3 Degree scale power
We believe that Fig. 1 shows a peak in power in the anisotropies at scales
around a degree. The precise position of this peak, how high it might
be, and whether it contains any substructure, are not so clear
(see e.g. [Scott, Silk & White 1995, Hancock et al. 1997, Lineweaver 1998, Bartlett et al. 1998, Bond, Jaffe & Knox 1998, Tegmark 1998]).
However, it is striking that this feature is in the general location of the
main acoustic peak predicted by currently favoured models, based on the
angular size of the horizon at last scattering.
It is worth stressing that this prediction was made more than a decade before
the experiments were performed (see for example [Doroshkevich, Zel'dovich & Sunyaev 1978]).
We expect the location of the peak to be determined definitively quite soon,
by upcoming ground based and balloon experiments, interferometers and
MAP, leading to very strong observational constraints on the angular
diameter distance back to last scattering ( ![]() ).
).
2.A.4 Polarization
It is a fundamental prediction of the gravitational instability paradigm that the CMB anisotropy is linearly polarized. In inflationary CDM-like models the level of polarization is a few percent of the anisotropy, and thus extremely small in absolute terms. There are already many limits on the polarization of CMB anisotropy (see [Hu & White 1997] for a list), however they are all nearly an order of magnitude larger than the theoretical predictions. The fact that the CMB is not `very' polarized tells us important information about the conditions at the last scattering epoch. That the CMB is not very circularly polarized, for example, indicates that there were no large magnetic fields present at last scattering (see also §2.B.4), although we are only aware of very stringent upper limits at the smallest angular scales ([Partridge et al. 1997]).
2.B.1 Inflation
We put this item at the very top of our `B'-list since we feel the weight of evidence is becoming very strong for something akin to inflation (for a discussion of whether inflation is really a testable theory, see [Barrow & Liddle 1997]). To avoid semantic arguments, it is important at the outset to be clear about the meaning of `inflation'. Here we refer to a period of accelerated expansion in the early Universe. This is the only known mechanism for making an isotropic and homogeneous universe, and at the same time generates apparently acausal adiabatic fluctuations, i.e. fluctuations in spatial curvature on scales larger than the Hubble-length at a particular epoch. We do not intend `inflation' to carry the additional baggage of an inflaton field with a well-defined potential, connected with particle physics, etc., although ultimately we would all like to see the mechanism of inflation find a realization in a well motivated theory of fundamental physics.
The amplitude and power spectrum of CMB anisotropies from degree-scales
up to the largest scales probed by COBE seem to indicate that super-horizon
size adiabatic fluctuations exist.
Our first hint comes from the normalization of the large-scale anisotropies
relative to the matter (see e.g. discussion in [Scott & White 1996]).
On dimensional grounds we expect that the amplitude of the temperature
fluctuations be ![]() where
where ![]() is the large-scale gravitational
potential.
In adiabatic models a cancellation ([White & Hu 1997]) between intrinsic
anisotropies and gravitational redshifts means that the coefficient is
reduced to 1/3, i.e.
is the large-scale gravitational
potential.
In adiabatic models a cancellation ([White & Hu 1997]) between intrinsic
anisotropies and gravitational redshifts means that the coefficient is
reduced to 1/3, i.e. ![]() ([Sachs & Wolfe 1967]).
In the simplest isocurvature models the coefficient is 2.
Since, as we mentioned before, our currently popular theories `work', there
is little room to absorb a factor of 6 in relative normalization.
Of course this alone is not proof of adiabatic fluctuations.
([Sachs & Wolfe 1967]).
In the simplest isocurvature models the coefficient is 2.
Since, as we mentioned before, our currently popular theories `work', there
is little room to absorb a factor of 6 in relative normalization.
Of course this alone is not proof of adiabatic fluctuations.
Our next piece of observational evidence is the angular scale of the `peak' in power. The structure of the peaks (locations, separations, relative heights) is a strong discriminator between adiabatic and isocurvature models ([Hu & White 1996]). In almost all isocurvature models the peak is shifted to smaller angular scales. Since we observe excess power at about the right place for adiabatic fluctuations in a flat universe, there is little room for either spatial curvature or isocurvature fluctuations (and the combination is particularly disfavoured!). Since the current evidence for a peak, in contrast to a rise, is modest we have put this in our `B'-list. The observational situation is likely to change rapidly. In the future we can hope that detection of polarization on degree scales will finally pin down the fluctuation type beyond any argument ([Hu, Spergel & White 1997, Hu & White 1997]), but this is a difficult measurement due to the low levels of signal.
Thus there is reasonable evidence
for adiabatic fluctuations in a spatially flat
universe. The latter has long been hailed as a `prediction' of inflation.
The former is also tantamount to a `proof' of inflation, in the sense that
the only causal means for generating nearly scale-invariant adiabatic
fluctuations is a period when ![]() in the early Universe
(see e.g. [Hu, Turner & Weinberg 1994, Liddle 1995]).
Of course this condition is neither entirely necessary nor sufficient.
On the sufficiency side, it is no doubt possible to imagine inflationary
models which have fluctuations of an entirely different character, but it
would seem pathological to deliberately avoid explaining density perturbations.
And on the necessary side, one could in principle imagine some early Universe
physics which somehow mimics the effects of inflation by producing
super-horizon adiabatic modes, and yet is not inflation.
We would argue that this is a purely semantic distinction:
if it looks like inflation and smells like inflation, then let's
call it inflation while leaving open the possibility that current
inflationary ideas may one day be shown to be part of some better paradigm.
In the same vein it may also be argued that some Planck-era physics somehow
generates apparently acausal modes. Again we would say that is either
isomorphic with inflation, or simply an attempt to push the question of
initial conditions into the realm of metaphysics.
in the early Universe
(see e.g. [Hu, Turner & Weinberg 1994, Liddle 1995]).
Of course this condition is neither entirely necessary nor sufficient.
On the sufficiency side, it is no doubt possible to imagine inflationary
models which have fluctuations of an entirely different character, but it
would seem pathological to deliberately avoid explaining density perturbations.
And on the necessary side, one could in principle imagine some early Universe
physics which somehow mimics the effects of inflation by producing
super-horizon adiabatic modes, and yet is not inflation.
We would argue that this is a purely semantic distinction:
if it looks like inflation and smells like inflation, then let's
call it inflation while leaving open the possibility that current
inflationary ideas may one day be shown to be part of some better paradigm.
In the same vein it may also be argued that some Planck-era physics somehow
generates apparently acausal modes. Again we would say that is either
isomorphic with inflation, or simply an attempt to push the question of
initial conditions into the realm of metaphysics.
2.B.2 Space-time structure
We have already mentioned that the extreme isotropy of the CMB is a strong
indication that the FRW metric is an excellent approximation to the large-scale
properties of space-time.
Strong quantitative limits on the rotation and shear of space-time for
specific Bianchi models have been obtained from the COBE data
([Bunn, Ferreira & Silk 1996, Kogut, Hinshaw & Banday 1997]). And limits on the geometry for general models
can be placed at the ![]() level ([Smoot 1991]).
level ([Smoot 1991]).
CMB anisotropies probe the Universe on the largest accessible scales, and so they also constrain things like the large-scale topology. There are quite stringent constraints in the simplest background models ([Stevens, Scott & Silk 1993, de Oliveira-Costa, Smoot & Starobinsky 1996]). However, in principle there may yet be observational consequences for compact topologies, in an open universe in particular ([Levin et al. 1997, Cornish, Spergel & Starkman 1998, Souradeep, Pogosyan & Bond 1998]). Exactly how stringent the current constraints are, for general classes of cosmology on the largest scales, is still a matter of debate. Nevertheless, we probably know at this point that the Universe isn't very strange on Gpc scales, quite an advance over our previous ignorance.
2.B.3 Gravity waves
If whatever produces the initial density perturbations doesn't discriminate on the basis of perturbation type we would expect that scalar, vector and tensor fluctuations would be produced at early times in roughly equal amounts. The vector modes, representing fluid vorticity, decay with time and so would not be present after a few expansion times. Thus we would expect today to see only scalar (density) perturbations and tensor (gravity wave) perturbations. Both of these types of perturbation would give rise to large-angle anisotropies, though only the former will seed large-scale structure. Due to the aforementioned close consistency between the amplitude of the clustering on galaxy scales and the anisotropy seen by COBE there is a limit to how much the gravity wave signal can contribute to COBE. Roughly speaking, the tensor to scalar ratio T/S<1 (see [Salopek 1995, Markevich & Starobinsky 1996, Zibin, Scott & White 1999]). If the tensor perturbations are not too different from scale-invariant this means that the possibility of seeing primordial gravity waves with detectors such as LIGO or LISA is small ([Krauss & White 1992, Turner 1997, Liddle 1994, Caldwell, Kamionkowski & Wadley 1999]).
As has been argued by Lyth ([Lyth 1997]), the low-level of gravity waves is good news for our current ideas about realizing inflation in simple particle physics inspired models. In the most popular models today, the scalar modes are expected to dominate over the tensor modes by many orders of magnitude. The expectation is therefore that the tensor signal may not be measurable with any existing or planned experiments, or conversely that a positive detection of gravity waves would have profound implications for our ideas about inflation. However, for the time being, the constraints on the gravity wave contribution have not reached the level where we learn much about early Universe physics - that will await future experiments.
2.B.4 Physics at ![]()
It is possible to use the fact that the CMB anisotropies are largely as
expected to limit the magnitude of any surprises at the last-scattering
epoch. The arguments are much akin to those using the observed abundances
of the light elements and Big Bang Nucleosynthesis theory to limit `exotic'
physics at early times. If something `exotic' would dramatically alter
the theoretical predictions, it can be strongly constrained.
A great many possible physical effects have been studied, but here we will
list only a few things for which it is already possible to place observational
bounds. Strong limits exist on domains of anti-matter ([Kinney, Kolb & Turner 1997]),
particle decays near ![]() ([Pierpaoli & Bonometto 1998]), primordial voids from an
early phase transition ([Sakai, Sugiyama & Yokoyama 1997]) and primordial magnetic fields
([Barrow et al. 1997, Subramanian & Barrow 1998]), among other things.
([Pierpaoli & Bonometto 1998]), primordial voids from an
early phase transition ([Sakai, Sugiyama & Yokoyama 1997]) and primordial magnetic fields
([Barrow et al. 1997, Subramanian & Barrow 1998]), among other things.