1.3 The Motion of the Sun and the Stars

Where ever you stand on the Earth (except for at North and South poles - we will come back to this later), the stars RISE in the EAST and SET in the WEST. That is, the APPARENT motion of the stars is moving east to west. The ACTUAL motion is that the Earth is spinning on its axis. The stars are fixed (at least on the time scale of the Earth's 24 hour daily spin). For the next couple of sessions we will be concerned about the APPARENT motion of the Sun, stars and Moon to an observer standing on Earth. These APPARENT motions are due to the fact that the Earth is spinning on its axis, that the Earth is orbiting the Sun and that the Moon is orbiting the Earth - the ACTUAL motions. The ACTUAL motions are the ones we would observe if we could step of the Earth, zoom out and look at the Earth - Moon - Sun system from afar.

Home Experiment

In this experiment you can use a piece of string with a weight on the bottom as a simple sundial, and measure the motion of the Sun.

The Celestial Sphere

Let's start with a celestial sphere and the Earth as in Figure 1.7. If we extend the North and South poles of the Earth outward until they intersected the sphere, the intersection points are defined as the North Celestial Pole and the South Celestial Pole. These always point back to the North and South poles on the Earth. Thus if you were standing at the North Pole and looked straight up, you would be looking at the North Celestial Pole in the sky. If you were at the South Pole, you would see the South Celestial Pole directly overhead. Similarly if we took the Earth's equator and projected it outward until we get to the celestial sphere, we would end up with a ring called the Celestial Equator. If you were at the equator, the Celestial Equator would be directly overhead in the sky at all times. The star Polaris is located very close to the North Celestial Pole. As a result, as the Earth rotates about its axis in its diurnal cycle, all the stars appear to rotate about us in the sky except for Polaris which stays fixed in its position near the North Celestial Pole.

(1) Go outside and find Polaris and the celestial pole in the night sky. The easiest way is to look roughly north and use the 2 "pointer stars" of the Big Dipper. (2) Point with your left arm to Polaris. Make a right angle to your left arm with your right arm. Your right arm is now pointing to somewhere on the celestial equator. Keeping your left arm pointing to Polaris and your right arm at a rightangle, rotate about your left arm--your right arm will be sweeping out the celestial equator. (3) Point to the south celestial pole. (4) Look for a bright star (preferable 2 or 3 different ones) that is fairly close to the horizon or an object on the skyline--such as the roof of a house or a tree or a lampost. Note where you are standing, where the star is located and the time. Come back in about 1 hour and note how the stars have moved.

Angles

Astronomy involves thinking about angles--often very tiny, tiny angles. A circle is divided into 360 degrees (or 360°). Each degree is divided into 60 arcminutes (or 60'). Each arcminute can be divided into 60 arcseconds (or 60"). Therefore there are 360x60x60 = 1,296,000 ~ 1.3 x 10⁶ arcminutes in a full circle. Yes, this seems a crazy system and not very `metric'--it goes back to the Babylonians who were hung up on the number 60. No one has been bothered to convince everyone else to make a better system. Try these exercises to get a feel for these angles.

(5) Hold your hand out at arms length (preferably against the sky towards the Big Dipper at night). Think of the long, skinny triangle made by the width of your fist and your eye. The width of your fist subtends and angle of 10° at your eye. The Big Dipper is about 20° (two fists at arms length) from end to end in the sky. (6) Now hold up a finger at arms length. The width of your finger subtends an angle of about 2° at your eye. So one degree would be about 1/2 a finger (or about the width of your little finger nail). Imagine dividing that angle into 60 arcminutes--or 3600 arcseconds--tiny angle, eh? (7) Think of a place (shop, house, landmark, etc.;) that is about 2.5 miles (4 kilometers) away. Imagine someone holding up a penny there. If you could see that penny 4 kilometers away, the angle the penny subtends at your eye is one arcsecond. This is the sort of tiny angle that astronomers like to work with.

Daily (or Diurnal) Motion

(8) Go back outside and note the motion of the stars. When you are facing Polaris, which way do the stars appear to go around the celestial north pole? (9) Face (a) east, (b) south, (c) west--in each case, describe the way the stars move over the night.

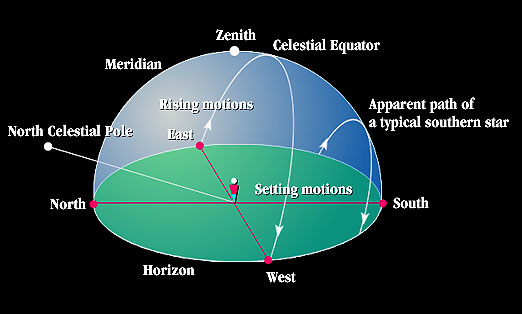
The Earth spins on its north-south axis which gives us day and night. If all the stars were fixed on the celestial sphere, then as the Earth spun, we would see that during different times of the day, we would see different parts of the sky or different parts of the celestial sphere. This is illustrated on the right (B) below.

Another way to look at this is if we assumed the Earth was stationary and if we have the celestial sphere rotating about the axis defined by the North and South Celestial Poles. This is in fact what we apparently see when we go outside and view the heavens. We appear to stand on an immobile Earth while all the stars and the Sun rotate around us. Thus the diurnal motion of day and night can be imagined to be due to the rotation of the celestial sphere around the Earth. This is illustrated on the left (A) below.

It is the apparent rotation of the celestial sphere that results in the Sun and stars rising in the east and setting in the west.

How do we KNOW that the apparent motion of the stars is due to the Earth spinning? The space-age view of the Earth as a "spinning blue marble" make this obvious. But before the space age it was not so clear. There was little concrete evidence to distinguish which of the following views was reality. A clever way of actually demonstrating the Earth's spin was devised by the French physicist Foucault who hung a huge pendulum that kept swinging for several hours. The pendulum keeps swinging to and fro in its initial direction and the Earth spins underneath. There is a Foucault pendulum in the Gamow Tower (opposite the stadium, across the road from the Ralphie statue) on the CU Boulder campus.

Apparent Motion of the Stars

This link shows you the apparent motion of the stars as viewed from a northern latitude location, at the equator, and a southern latitude location. For each location, we see the motion of the stars in the four cardinal directions: North, East, South, and West. Each animation shows you a winter sky through an entire day, with the Sun and Moon "turned off" so you can watch the stars move.

Annual (or Seasonal) Motion

(10) What do we call the line that passes through the signs of the zodiac? (11) What celestial object follows this line? (12) Why do people talk about "winter constellations" or "fall constellations", etc.?

Back to Figure 1.10. Notice that the ecliptic is tilted with respect to the celestial equator. This is due to the fact that the Earth's axis is tilted 23.5° with respect to the plane of its orbit. From the perspective of a stationary Earth, it would appear that the ecliptic is tilted 23.5° with respect to the projection of the Earth's equator.

Note that the Earth's orbit is very close to circular. The distance of the Earth from the Sun only varies by 4% over the year. Furthermore, the Earth is closest to the Sun in January - which is summer for the southern hemisphere but winter for the north.

With an Earth tilted 23.5° with respect to the ecliptic, the Sun will appear at different elevations, or angle above the horizon, at different times of the year. This variation in the elevation of the Sun over the year is the cause of the seasons.

The following diagram shows the elevation of the Sun at different times of the year in Boulder. Polaris is always 40° above the northern horizon in Boulder (same as Boulder's latitude). The celestial equator is also always fixed at 50° above the southern horizon. During the course of the year, the Sun will move 23° to the north of and to the south of the celestial equator. It will be furthest north during the summer solstice; it will be furthest south during the winter solstice.

Figure 1.12 shows some of the constellations of the zodiac projected onto the celestial sphere. Notice gemini, pisces (which is 'in front'), sagittarius and virgo (which is 'at the back'). Now look at Figure 1.10 which shows the ecliptic. The ecliptic in the diagram marks the path that the Sun takes in the sky. If we were to view the Solar System from the outside, the ecliptic would actually be the plane of the orbit of the Earth about the Sun. From our normal perspective from the Earth however, the ecliptic appears as the path that the Sun takes over the year through the constellations of the zodiac.

Remember that the Sun appears to be in different constellations of the zodiac at different times of the year because the Earth is orbiting the Sun. In Figure 1.10 of the celestial sphere, this would correspond to the Sun moving along the ecliptic, making a complete circuit once a year. Remember that the celestial sphere encompasses the entire sky!

Celestial Coordinates (See page 10)

The star Polaris is located very close to the North Celestial Pole. As a result, as the Earth rotates about its axis in its diurnal cycle, all the stars appear to rotate about us in the sky except for Polaris which stays fixed in its position near the North Celestial Pole. This fact gives us the ability to figure out our latitude on the Earth by looking for Polaris: To measure latitude on the Earth, measure the angle between Polaris and the horizon.

Thus if you were to stand at the North Pole, the North Celestial Pole would appear directly overhead to you, and Polaris would be overhead as well. The angle between what's directly overhead and the horizon is a right angle, or 90°. Thus your latitude is 90° North.

If you were at the equator, Polaris would appear to be on the horizon towards the north. Their is thus no difference between its position and the horizon, that is, its angle is 0°. Thus we are at a latitude of 0°.

For us living in Boulder, if we were to go out in the night and measure the angle of Polaris above the horizon, we would find it to be 40°.

(13) How would you measure your latitude if you were in Australia? Would you be able to see Polaris? What would you use instead of the North Celestial Pole to aid you in navigating? Is there a star close to the South Celestial Pole like there is a star near the North Celestial Pole?

Longitude, an east-west measurement is a little harder. For latitude, we had the equator and the North and South Poles as reference points. We can talk about being some number of degrees north or south of the equator. For locations east or west, there isn't any obvious natural reference position.

As a result, we have invented a 0 degree longitude position. This is defined to be a line running north-south through Greenwich, England, which is near London. All geographic locales on the globe have longitudinal positions relative to Greenwich. Boulder happens to be 105° West.

So how do we tell how far east or west we are from Greenwich? Let's look at the following diagram:

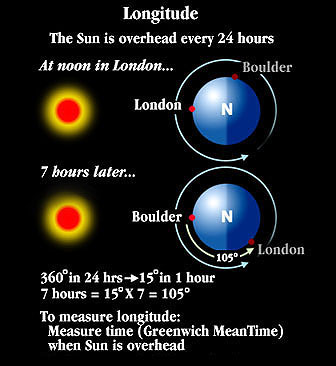
We have to remember that the Earth is rotating about its axis and that the Sun appears overhead once every 24 hours at every place on the Earth. In the diagram above, we are looking down on the Earth's North pole. An arrow shows the direction of the Earth's rotation. The Sun is directly overhead in London (making it noon there), while in Boulder, the Sun hasn't even risen yet since Boulder is still on the nighttime side of the Earth.

In the next diagram, we are now 7 hours later. The Earth has rotated bringing Boulder into a position where the Sun is now overhead in Boulder. For Londoners, the Sun has just set since now London is on the nighttime side of the Earth.

Since we know the Earth has to rotate completely in 24 hours, and one entire rotation means circling 360°, the rate in degrees that the Earth rotates per hour is:

                 360 degrees     15 degrees
Rotation rate = ------------- = ------------
                   24 hours         hour

Or 15° per hour. Since it took 7 hours before Boulder rotated to have the Sun overhead, then number of degrees that it rotated must have been:

                                  15 degrees
Total amount rotated = 7 hours x ------------ = 105 degrees
                                     hour

Boulder is thus 105° West of Greenwich. To summarize, what we did was to time the difference between when the Sun was overhead at Greenwich and when it was overhead in Boulder to figure out the longitude. Thus if you wanted to navigate while sailing across the ocean, you needed to have a good clock, since you needed to know the time in Greenwich.

(14) What is the longitude of the International Date Line? (15) Hawaii is at a longitude of 157° . How many hours is Hawaii ahead or behind Boulder?

READING RECOMMENDATION: The story of the race to develop an accurate method of measuring longitude is very well told by Dava Sobel in an excellent little book called Longitude: the True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time (1996, Penguin USA). The story is of John "Longitude" Harrison, who solved the problem of determining east-west position, something that both Newton and Galileo had failed to do, by inventing a clock that could withstand the pitching and rolling motions of a ship on the ocean, the temperature and humidity variations, and keep perfect time. I am afraid that the astronomers did not behave well on this occasion.

Links: Earth and Moon viewer, a site that lets you view the Earth and Moon from a variety of angles - at specific times (e.g. right NOW). Includes up-to-date weather satellite images. How to Find Your Directions in the Sky, a page from a Metro State College Denver astronomy class, contains more details about determining where you are on the Earth. Planisphe re at Otterbein College. You can download either PostScript or PDF files that will allow you to create your own planisphere, which tells you the positions of stars in the sky at different times of the year. For the Boulder-Denver area, be sure to download the version for a latitude of 40°.

Celestial Latitude and Longitude.
On page 10 there is a box that describes the celestial coordinates. There are angles like longitude and latitude on the celestial sphere that describe the location of a star, such as Betelguese. These angles are called Right Ascension and Declination. We will not use these coordinates in this course but you should know that astronomers use them to describe the locations of objects in the sky.

Sundial Home Experiment

If you live near the Boulder campus or have access to a sundial, you can do an exercise that leads you apparent motion of the Sun.

Links: Sundial page from the Royal Greenwich Observatory.