| DATE |
Lecture
22 |
| TITLE |
The
Expanding Universe |
| READING |
Chapter
18 |
| MAIN
CONCEPTS |
Hubble
Law, Density and Curvature of Universe |
COURSE
NOTES:
Hubble
Expansion
Once
the nature of the spiral nebulae was uncovered, the next astounding fact
about them turned out to be that they are moving away from us, some at
very high speeds. Hubble used his work on calibrating extragalactic distances
together with the measured redshifts to find the expansion of the Universe.
This turned out to follow a very simple law: velocity=distance*Hubble
constant. The Hubble constant is the slope of the line which relates
distance and velocity. It has units of velocity/distance; one can use (km/s)/ly
or (km/s)/Mpc (then the distance has to use the right units).
This
law arises because the scale
of the Universe is expanding; the distance between any 2 points changes
by the same scale factor in a given amount of time. If the distance is
small and it doubles, it changes by twice a small amount. If the distance
is large it changes by twice a large amount in the same time. Since velocity
can be expressed as the change in distance per unit time, you can see that
far away objects will appear to have a large velocity given this law. Once
we know the value of the Hubble constant, one need only measure the redshift
of an object and the Hubble law will yield its distance. The Hubble flow
is only important on the scale of millions of ly, and is invalid for any
systems which are gravitationally bound together (the gravity can resist
the tendancy of space to expand). The "velocity" of expansion does not
reflect motion through space, but motion caused by the expansion of space.
It is therefore not subject to the restriction of the speed of light, and
can have any value.
The
size and age of the observable Universe can be found when the Hubble expansion
is understood. The best way to see its relation to the age is to imagine
reversing time. Now the Universe is everywhere contracting instead of expanding,
and the distances between things is constantly decreasing. Obviously, if
you run this "movie" long enough the scale of the Universe will shrink
to zero! The time it takes to do that is the age of the Universe. If the
Hubble constant really were constant, then the age would be given by its
reciprocal (1/H); you can see that the units work out that way: 1/H ~ dist./
(dist./time) ~ time. With our best estimate of the value of H (from observing
distance galaxies and measuring their redshift and having an independent
way of estimating their distance) we find an age of about 14 billion years.
This agrees well with the ages of the oldest globular clusters, which seem
about 13 billion years old.
The
size of the observable Universe is then given by the distance light can
have travelled since the beginning, namely 14 billion light years. The
"true" Universe could be much bigger than that (and we think it is), but
that is the "horizon" over which we cannot see. As we look out toward
this horizon, we are also looking back in time, since the light we see
from far away has taken a very long time to reach us. Thus, it is possible
to review the history of the Universe by looking further and further -
by building bigger telescopes to view fainter objects we are building time
machines with greater reach into the past. We currently can see back to
the era when galaxies were being assembled, with optical and infrared telescopes.
We actually see much further back than that, to the time when the Universe
first became transparent, when we observe the cosmic
microwave background.
The
Hubble constant need not have been constant for the whole history of the
Universe. Since there is mass/energy in the Universe, there is a gravity
associated with it. This will cause the expansion of the Universe to slow
with time, just as a ball thrown into the air slows its upward flight.
Correcting for this effect reduces the age estimated from the current Hubble
constant by 1/3 if the Universe will eventually slow to a stop (which would
be in conflict with the globular cluster ages). This is fixed, however,
if the Universe is now accelerating (as
recent results suggest). There are three possibilitites for the overall
curvature of spacetime in the Universe: it can be closed,
flat, or open.
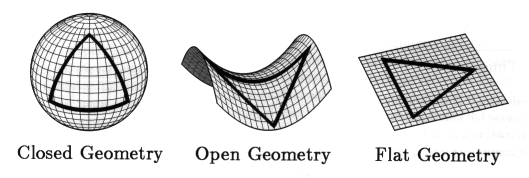
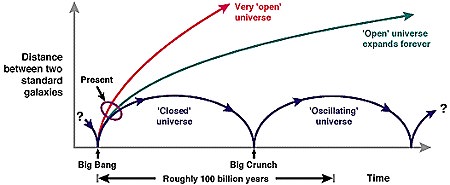
These
correspond to three eventual fates: it can recollapse after some (large)
time, the expansion can slow to a halt after an infinite time, or the expansion
can go on forever at some rate. Since the amount of gravity determines
the curvature, and matter makes gravity, there is a "critical
density" which corresponds to flatness. We think that the geometry
of the observable Universe must be flat, because of the inflation hypothesis.
Observations of the Cosmic Microwave Background appear to be providing
accurate confirmation of this. Actually, things have gotten more complicated
since the discovery
using Type I supernovae that the expansion of the Universe may be accelerating.
This would be due to a kind of "cosmic antigravity" (akin to Einstein's
cosmological constant). In that case, the Universe can be flat, but could
expand as though it were very open (galaxies within our horizon today can
be pulled beyond it by this accelerating expansion). Either way, the Universe
will end up very empty and cold. Cosmology is now both a theoretical and
observational science with increasing precision; the important
parameters of our Universe will be fairly well known by the end of
the first decade of the 21st century.

