The Im & Stockman Deep Field

A Deep Observation with IFIRS

We have taken Im & Stockman's simulation of a blank field at very low flux levels to demonstrate the spatial multiplex advantage of IFIRS. In this simulation we have shown only 0.02% of the field of view of IFIRS. If we had simulated the entire data cube it would contain spectra for tens of thousands of galaxies.

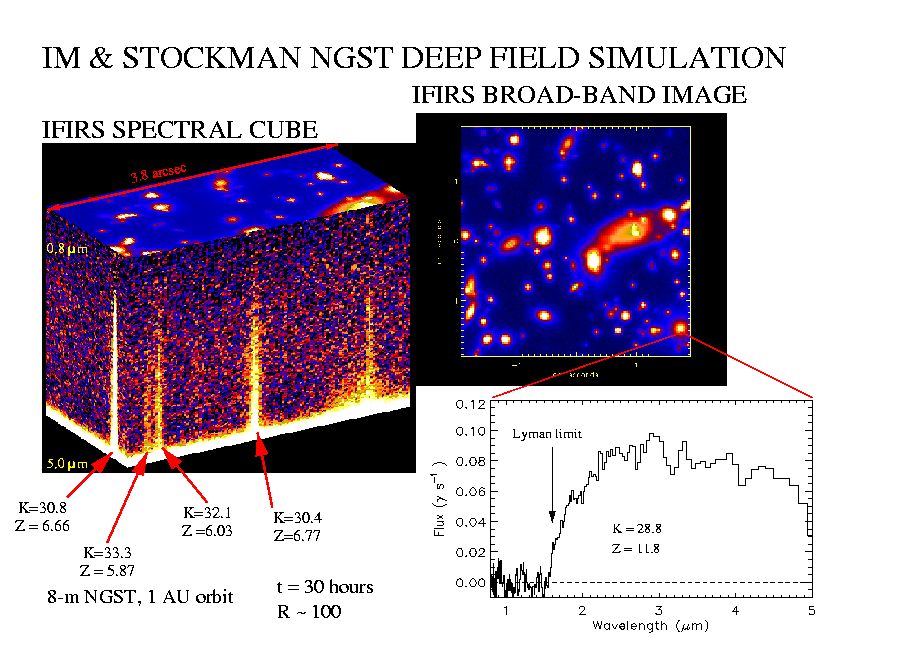
Unlike the simulation of star forming galaxies the spectral energy distributions omit nebular emission lines, so redshifts must be deduced from stellar absorption features and spectral breaks. In this example objects with K = 31.3 AB mags are detected with SNR = 5 per spectral resolution element, which is sufficient SNR to identify the Lyman break in objects as distant as z = 12.

Comparing an IFTS & a Multi-Object Spectrometer

Using the Im & Stockman simulation we can compare the performance of a multi-object spectrometer (MOS) and an IFTS for the following experiment related to the galaxy evolution DRM. The goal of the experiment is to obtain the spectra of the greatest number of faint galaxies that can be observed in the total allotted integration time.

The following argument suggests that an IFTS is the best instrument for this measurement. Define the relative speed of an IFTS to a MOS as the ratio of the number of galaxy spectra obtained with each instrument in a fixed observing time (same wavelength range and number of spectral channels in each case). For background limited operation a Fourier transform spectrometer is R times slower than a dispersive spectrometer for a single object, where R is the spectral resolution. However, the FTS can obtain a spectrum for every object in the field of view, and hence has an enormous spatial multiplex advantage over a slit spectrometer. If the integral galaxy number counts scale as flux^-a, then the speed of the IFTS compared to a MOS is proportional to

f₀^-a/(N_slit R),

where f₀ is the faintest galaxy with a recorded spectrum. N_slitis the number of MOS slits (assuming one object per slit). Since the predicted value of a is about 1, the conclusion is that at faint enough flux levels the IFTS always wins. In the real world the dispersive instrument will be detector limited by read noise and dark current and the advantage will be even greater.

Consider a specific example where we can include more real-world factors. Since the objective is to observe as many faint galaxies as possible the IFTS observation is conducted by using the entire integration time interval to observe one field. Multiple fields are observed with the MOS so that the number of MOS pointings times the integration time per pointing equals the time allocated to the IFTS observation. The surface density of galaxies is derived from the Im & Stockman simulations which are normalized to deep NICMOS counts. The total number of galaxies with spectra with SNR > 10 are plotted on the y-axis.

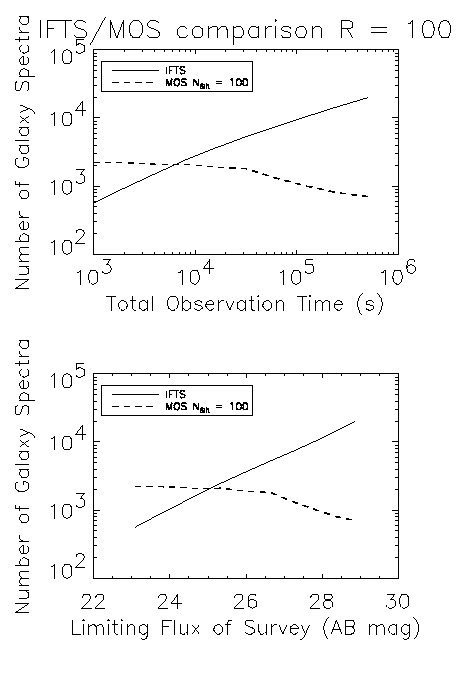
These plots are two projections of a single 2d surface.

The parameters adopted for this comparison

IFTS FOV = 5.'28 x 5.'28
N_slit = 100 for the MOS
Spectral resolution R = 100
Wavelength range = 1.3 - 2.6 micron (i.e. the FSR of a m=1 grating blazed at 2 microns)
Dark current = 0.03 e^-/s
Read noise = 5.0 e^- rms read noise
t_max = 1800.0 sec maximum time before readout to veto cosmic rays

The MOS reaches the stage of diminishing returns at K ~ 25 AB mags or an integration time of ~ 10,000 seconds. Beyond that the IFTS is a clear winner, if the number of galaxies with observed spectra is the figure of merit.

This makes the IFTS look very good. The more investment you put into the IFTS survey the more you get because the slope of the integral galaxy number counts is steep. In particular the IFTS is very good at finding rare types of faint galaxies (perhaps these will be the most distant objects).

Back to the Berkeley NGST page.