The signal-to-noise performance of 3-d imaging spectrometers equipped with 2-d detector arrays is the same for all architectures, in the ideal case of photon shot noise limted operation. This is correct so long as the spectrometers are equipped with the same size arrays, and the same spatial and spectral degrees of freedom of the astronomical scene are observed. A heuristic proof follows, a more formal derivation is given by Bennett (2000).
For ideal instruments, making use of 2-d detector focal plane array's
(FPAs), this parity is obtained under the conditions that the only limitation
on SNR is pure white quantum statistical noise for each of the possible
designs, that all systems enjoy equal total exposure times and entrance
aperture sizes, and that the F/# referred to the cone of light converging
on the FPA detector elements is the same for all designs. For simplicity,
the target specific intensity radiance is assumed to be constant over a
bandpass B, and constant over the imaged area A. For each imaging spectrometer
design, the ideal limiting SNR is calculated for a representative cell
in the 3-d data cube.
where 
is the source photon rate per unit wavenumber, 
is the system efficiency, including the telescope, collimator, beam-splitter,
and camera throughput and the detector QE. The integral is taken over the
full bandpass of the system. The signal-to-noise ratio in the time domain
is given, on average, by
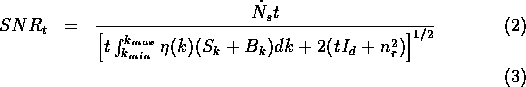
Where the noise consists of photon shot noise from source and background
photon rate, 
, dark current 
, and read noise, 
. The integration time per optical path difference (OPD) step is t.
The factor of two in dark and read noise occurs because of the twin FPAs
required for a four-port
instrument.
The relation between the signal to noise ratio in the spectral domain
to the signal to noise ratio in the temporal domain can most easily be
derived using Parseval's theorem. If there are 
frames in the interferogram the relation between the noise level in the
spectral domain, 
, to the noise in the time domain, 
, assuming that it is white is given by
Hence, the SNR in the frequency domain is
where the last equality is obtained under the assumption of a white spectrum extending over m spectral channels. The SNR for an IFTS at any given resolution simply scales as 1/m per spectral channel.
.
In the same amount of time required for the
samples by the Fourier transform instrument, a total of 
passes through the bandpass B may be made, leading to
where 
is the signal to noise ratio that would be obtained if the complete bandpass
B
impinged on the imager, and is equivalent to the corresponding value in
Eq. (1). An ideal TF is thus identical to and an ideal IFTS.
spatial lines in order to accumulate an entire data cube. Thus the ideal
SNR is given by
For a square FPA, the 
. Integral field unit spectrometers and multi-object spectrometers are
variants of the imaging DS, which slice the field of view in different
ways.
In the case that the same spatial and spectral elements are measured in the data cube, there is no difference in SNR between the three general designs of imaging spectrometers.
The demands on the detector FPA are substantially different between the approaches. In the IFTS, the individual frames are exposed to a much greater signal flux, and thus detector noise is less critical than for either the DS or TF.
Because of the higher signal flux, the IFTS can be operated in the mid-IR with warmer optics and detector housings. For mid-IR space applications, for which there is a premium on cryogenic mass, this is a great advantage.
For the TF it is possible to jump around in wavelength, and, in principle, one need only measure the bare minimum of spectral features needed to identify or quantify a given target.
The IFTS has the advantage of the greatest flexibility in terms of the choice of spectral resolution. With the current IFIRS design spectral resolution ranging 1-10,000 can be obtained with the same instrument.
In general, for a fixed observation time, the SNR per spectral channel varies in direct proportion to the width of the instrumental resolution. The IFTS enjoys the brightest imagery of any of the imaging spectrometer designs because the full band-pass is transmitted to the focal plane. This is advantageous if it is necessary to use the instrument for guiding.
The top example shows the spectrum from the distant star forming cluster at z=12 simulation assuming projected detector performance (5 e- rms read noise and 0.03 e- s-1 dark current). The bottom panel shows what could be achieved with current detector performance (30 e- rms read noise and 0.2 e- s-1 dark current). The signal-to-noise in each spectrum is limited only by the background and virtually uneffected by poorer detector properties.