Spectral Multiplexing 

Three Band Example

Consider the problem of color TV, where we want to record three wavelength bands. Suppose we have a single focal plane detector array and a filter wheel. The simplest way of recording the scene is to cycle between three filters, R, G, & B. We can improve on this scheme by using filters with broader band-pass that transmit more light , e.g, B + G, G + R, B + R Schematically, plots of transmission versus wavelength for these three filters, labeled m1, m2, and m3 would look like this:

We double the amount of light transmitted to the detector, but we have to do a little math to recover the images in the R, G, & B channels.

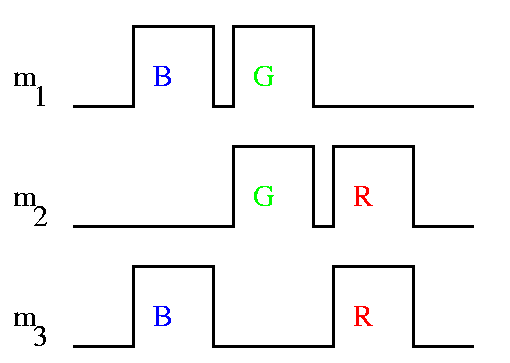
B = (m1 - m2 + m3)/2
G = (m1 + m2 - m3)/2
R = (-m1 + m2 + m3)/2

Clearly this has become a simple problem of linear algebra.

The Pan-Chromatic Image

In addition to the R, G, & B images, there is also a broad-band, or pan-chromatic image which we can form by summing,

X = m1 + m2 + m3 = 2(R + G + B).

Signal-to-Noise

If we are quantum limited, and the only noise source is photon counting statistics, then the variance in each band, S, equals the total number of photons.

S(m1) = m1,  S(m2) = m2,  S(m3) = m3.

Error propagation gives the variance in each synthesized band as,

S(R) = (m1 + m2 + m3)/4,  S(G) = (m1 + m2 + m3)/4,  S(B) = (m1 + m2 + m3)/4.

Thus the noise is the same for each band. For a flat spectrum, i.e., R =G=B and m1 = m2 = m3= m, and the signal-to-noise ratio (SNR) for each synthesized band is,

SNR(R) = SNR(G) = SNR(B) = ( 1/3 m )½.

Since the signal in any one of our filters, m1, m2, or m3, the ratio of SNRs in the synthesized bands for multiplexing versus the fixed filter is,

SNR(multiplex)/SNR(fixed filter) = ( 2/3 )½ = 0.817.

If the spectrum consists of an emission line in the R filter, and  G =B = 0, then

SNR(multiplex)/SNR(fixed filter) = ( 2 )½ = 1.414.

For the the pan-chromatic image in the case of a flat spectrum

SNR(multiplex)/SNR(fixed filter) = ( 2 )½ = 1.414.

How can we do better?

In this example the special filters only transmit two thirds of the total light. If we could transmit all the light to the detector all the time, then

SNR(multiplex)/SNR(fixed filter) = 1

and for the the pan-chromatic image

SNR(multiplex)/SNR(fixed filter) = N ½,

where N is the number of multiplexed spectral channels.

A four-port IFTS is efficient because it transmits all the light to the detectors all the time! This explains why an IFTS and a camera with a set of filters have have equivalent performance. However, the IFTS pan-chromatic image has a N½, SNR advantage over adding the individual camera filter images together. For a formal treatment and to better understand why an Fourier transform spectrometer is competitive with traditional instruments read Charles L. Bennett's contribution to the recent conference "Imaging the Universe in Three Dimensions: Astrophysics with Advanced Multi-Wavelength Imaging Devices".

Back to the Berkeley NGST page.