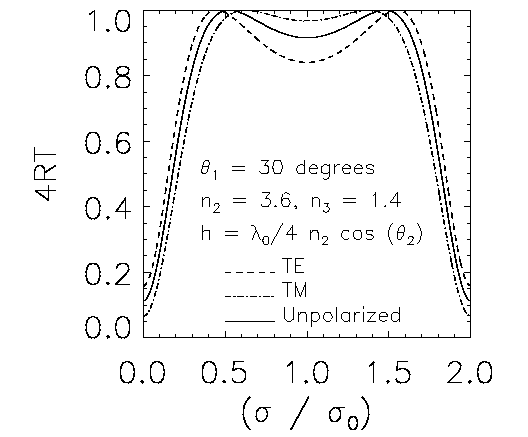Flexible Efficient & Practical 
Flexible
An IFTS is an electronically programmable filter which obtains spectra
for every pixel in the field of view. The imaging performance of IFIRS
is diffraction limited at 2 µm, and Nyquist sampled at 3 µm
in the near-IR channel and 6 µm in the mid-IR channel.
-
An IFTS performs the functions of several instruments
-
An IFTS is a camera or tunable filter
-
An IFTS is a multiobject spectrometer
-
An IFTS is an integral field unit
-
The spectral resolution of an FTS is continuously variable
-
The spectral resolution is set by the choosing the maximum optical path
difference scanned
-
For IFIRS the maximum path difference is 1 cm, hence the maximum
resolution is 104 at 1 µm
-
The free spectral range of an IFTS is theoretically infinite and in practice
is limited only by the working wavelength range of the beam
splitter and detector.
The SNR performance of a camera equipped with filters and an IFTS are equivalent
when they have perfect detectors. However, an IFTS has an extra degree
of flexibility because the pan-chromatic
image (i.e., the image formed by adding all the spectral channels together)
has a speed advantage over the filter camera equal to the number of bands
observed. For example, the Hubble Deep Field was observed with four filters.
The U+V+R+I image would have been twice as deep if obtained with an IFTS.
A camera equipped with a set of narrow band filters will become readnoise
and dark current limited.
Efficient
The efficiency of an ideal four-port
IFTS is 100%. Every photon is directed towards either one of two focal
plane detector arrays. The switching probability is a function of the optical
path difference and the wavelength of the light. An IFTS is a "black-box"
which sorts photons according to their wavelength.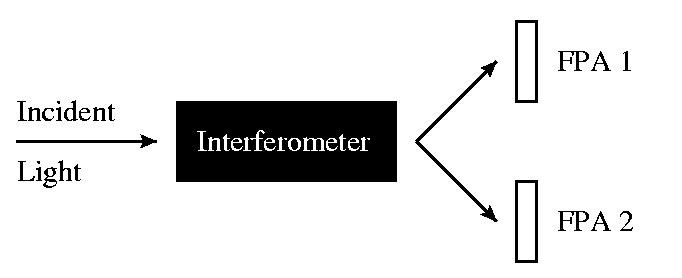
Thus when statistical noise dominates, the peformance of a 3-d imaging
spectrometer based on a 2-d focal plane array is the same for all architectures,
whether a camera with filters, a dispersive long-slit spectrometer, or
an imaging Fourier transform spectrometer. Of course, this only applies
when the same image cube is acquired with each instrument. To build up
the data cube the camera must cycle a set of filters and the dispesive
spectrometer must scan a slit across the field.
Ideal gratings do not have 100% efficiency. Even on blaze an ideal grating
has an efficiency of < 90% due to light lost in unwanted orders. The
exact number depends on the blaze angle, the order of interference, and
the opening angle between the incident and diffracted beams. When averaged
over the free spectral range this figure typically drops to 70%. Real grating
spectrographs also have slit losses, light scattered by irregularities
in the ruling, absorption in the grating coatings, and limited free spectral
range. A slit must also be used in a dispersive spectrometer. A grating
used in first order spans an octave in wavelength, so for diffraction limited
operation the slit can be matched to the image size at only one wavelength.
The slit is either too big or too small, which compromises the SNR. At
short wavelengths excess background light increases the photon shot noise,
and at long wavelengths slit losses reduce the signal.
An Ideal Beam Splitter
Real IFTS instruments are not 100% efficient because beam splitters are
not perfect. A perfect beam splitter has a relfectivity of 50% and a transmission
of 50%. This is impossible to satisfy over all wavelengths. The simplest
beam splitter, shown on the left, consists of a quarter wavelength high
refractive index material deposited on a substrate. 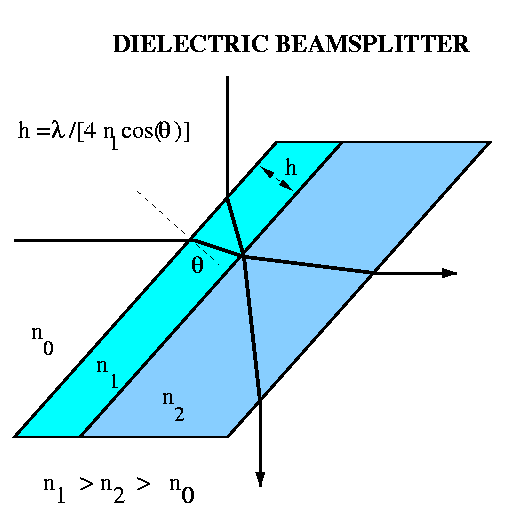 If R is the reflection coefficient, and T is the transmission
coefficient, a perfect beam splitter has an efficiency 4RT = 1.
The figure on the right shows the efficiency plotted versus relative wavenumber
for a simple single dielectric layer beam splitter (see Born & Wolf
p 61).
If R is the reflection coefficient, and T is the transmission
coefficient, a perfect beam splitter has an efficiency 4RT = 1.
The figure on the right shows the efficiency plotted versus relative wavenumber
for a simple single dielectric layer beam splitter (see Born & Wolf
p 61).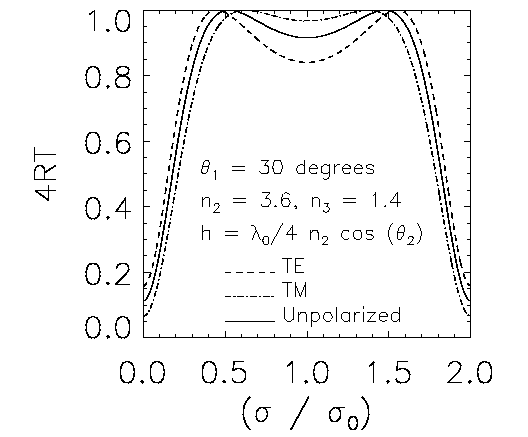
The reflectance of a beam splitter does not have to be precisely 0.5
to achieve high efficiency. If the beam splitter does not absorb, then
4RT
= 4R(R-1), so if 0.28 < R < 0.72, the beam splitter efficiency,
4RT
>
80%.
A simple beam splitter is efficient only over a finite wavelength range,
and in a practical IFTS it is this component that determines the useful
free spectral range. In this example, the free spectral range spans a factor
of 6 in wavelength. Compare this with a grating, where the corresponding
factor is (m+1)/m, where m is the order of the interference.
The best a grating can do is when m = 1, and the spectrum spans
an octave.
Real Beam Splitters
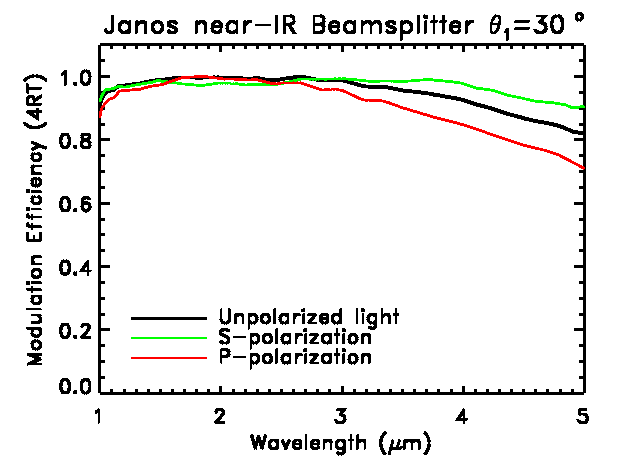
High efficiency mulitlayer beam splitters can be fabricated. The following
figure shows an example of a beam splitter designed and built by Janos
Technology Inc. for an FTS operating at 0.96-5.4 µm. The
modulation efficiency 4RT > 80% over the entire wavelength range.
A Fourier transform spectrometer equipped with this beam splitter would
have a free spectral range approching the theoretical limit of an ideal
beam splitter. Note, that unlike a grating, this beam splitter is only
weakly polarizing.
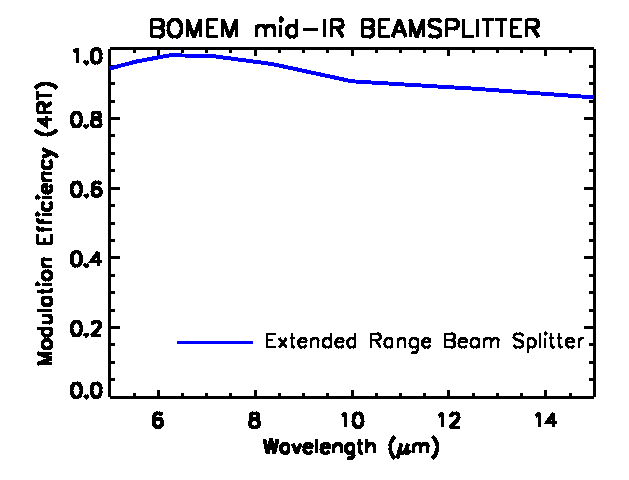
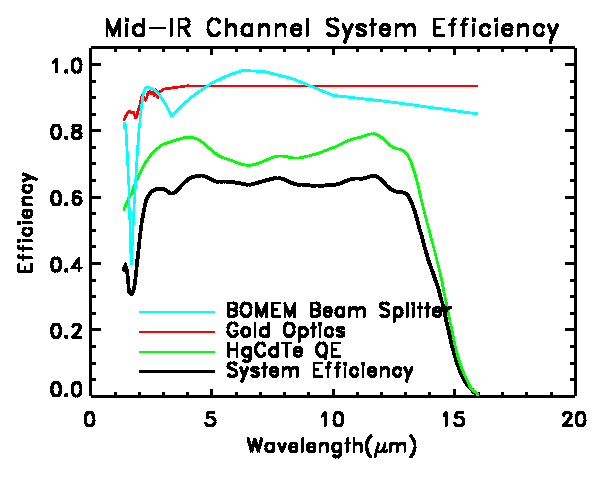
 For the mid-IR channel (5-15 µm) of IFIRS we have chosen a Bomem
beam splitter as characteristic of a high efficiency component.
For the mid-IR channel (5-15 µm) of IFIRS we have chosen a Bomem
beam splitter as characteristic of a high efficiency component.
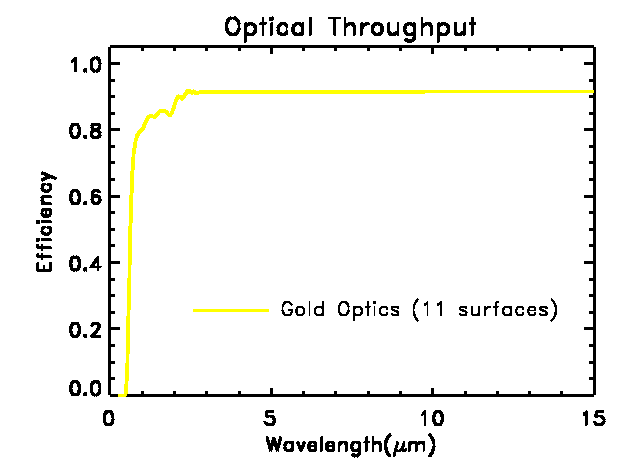
Optics
All reflective, diamond machined, metal optics will be used for IFIRS.
This ensures high image quality and high throughput. The reflectivity of
a single gold-coated surface exceeds 99% for wavelengths longer than 1.5
µm. The optical system of IFIRS consists of, a collimator, a camera,
two fold mirrors, cube-cornrer reflectors (three reflections) and a dichroic
to separate the near- and mid-IR light. The collimator and camera are both
three-mirror anastigmats, giving a total of eleven reflecting surfaces.
The corresponding throughput is plotted.
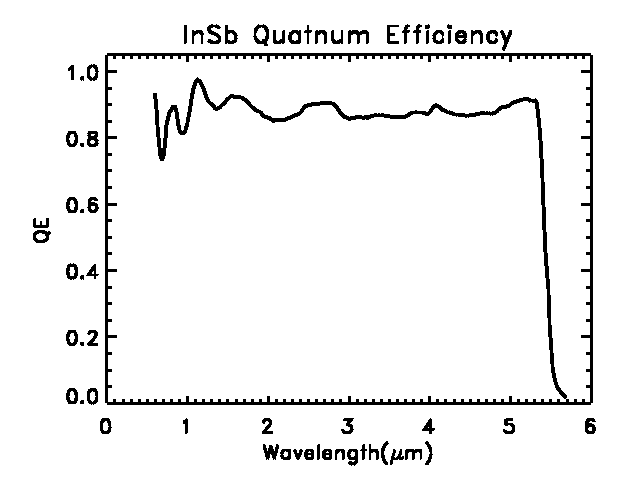
Detectors
IFIRS will use InSb and HgCdTe focal plane arrays. The near-IR channel
will be equipped with a InSb detector similar
the 1024 X 1024 Astronomy Focal Plane Array (ALADDIN) manufactured by Raytheon.
InSb arrays can be anti-reflection coated to give broad-band performance
from 0.6 µm to the detector material band-gap at 5.6 µm.
Hg1-xCdxTe
is used for the long wavelength channel. This detector material has the
advantage that the band gap can be tuned by between 3-30 µm by varying
the composition (i.e.
x) . Since dark current is a strong function
of temperature and the cut-off wavelength, the composition of Hg1-xCdxTe
can be selected for optimum performance at the operating temperature of
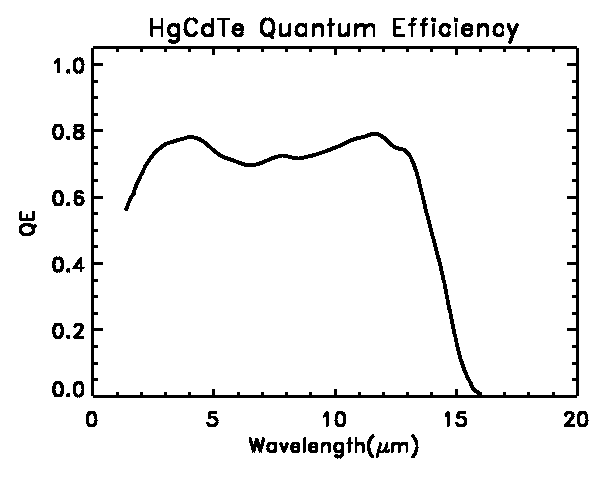
the passively cooled NGST instrument module (T ~ 30 K). This example shows
the QE curve for 14 µm cut-off HgCdTe, which is typical of longwave
detectors from the Rockwell
Science Center. (The true response is probably flatter than shown
here - the large scale ripple probably an artifact of the spectrometer).
System Efficiency
The efficiency is determined by the combination of the throughput of the
optics, the beam splitter efficiency, and the quantum efficiency of the
detector. The combination of these three factors is displayed in the plot
for the 0.96 - 5.4 µm Janos beam splitter and an SBRC InSb detector.
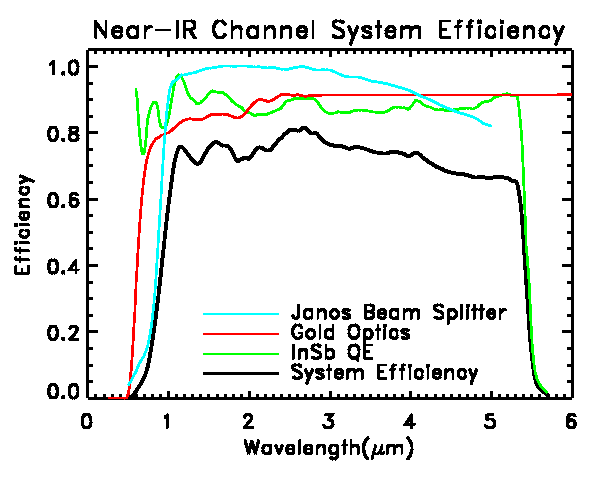 The efficiency is high and flat. The average in-band efficiency between
the half-power points is 73%. Over most of the wavelength range, the detector
dominates the losses. The ripples in the efficiency are due to the anti-reflection
coating on the detector. A similar plot is shown for the mid-IR channel.
The efficiency is high and flat. The average in-band efficiency between
the half-power points is 73%. Over most of the wavelength range, the detector
dominates the losses. The ripples in the efficiency are due to the anti-reflection
coating on the detector. A similar plot is shown for the mid-IR channel.
Practical
An IFTS is practical because it represents a marriage of proven technologies:
-
Large format focal plane arrays
-
Laser metrology & cryogenic actuators
-
High efficiency, wide-band, multi-layer beam splitters
-
Fast computers and data processing algorithms (e.g., Fast Fourier Transforms)
Back to the Berkeley NGST page.



 If R is the reflection coefficient, and T is the transmission
coefficient, a perfect beam splitter has an efficiency 4RT = 1.
The figure on the right shows the efficiency plotted versus relative wavenumber
for a simple single dielectric layer beam splitter (see Born & Wolf
p 61).
If R is the reflection coefficient, and T is the transmission
coefficient, a perfect beam splitter has an efficiency 4RT = 1.
The figure on the right shows the efficiency plotted versus relative wavenumber
for a simple single dielectric layer beam splitter (see Born & Wolf
p 61).