Vector perturbations represent vortical motions of the matter, where
and 
,
similar to ``eddies'' in water.
There is no associated density perturbation, and the vorticity is
damped by the expansion of the universe as are all motions that are not
enhanced
by gravity. However, the associated temperature fluctuations, once
generated, do not decay as both 
and T scale similarly with
the expansion.
For a plane wave perturbation, the velocity field 
with direction reversing in crests and troughs
(see Fig. 5). The radiation field at these
extrema possesses a dipole pattern due to the Doppler shift from
the bulk motion. Quadrupole variations vanish here but peak between
velocity extrema.
To see this, imagine sitting between crests and troughs.
Looking up toward the trough, one sees the dipole pattern projected
as a hot and cold spot across the zenith; looking down toward the
crest, one sees the projected dipole reversed. The net effect is
a quadrupole pattern in temperature with 
The lobes are oriented at 45 
from 
and 
since
the line of sight velocity vanishes along and at 90 degrees to
here. The latter follows since midway between the crests and
troughs itself is zero.
The full quadrupole distribution is therefore described by
,
where i represents the spatial phase shift of the quadrupole with
respect to the velocity.
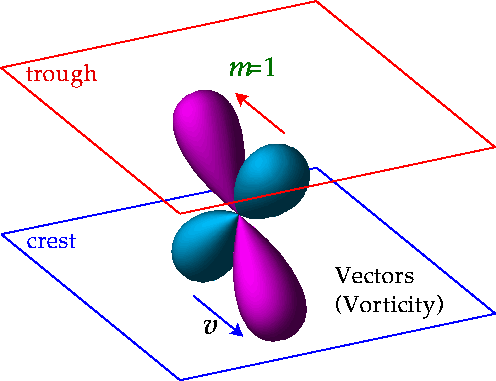
Thomson scattering transforms the quadrupole temperature anisotropy
into a local polarization field as before.
Again, the pattern may be visualized from the intersection of the
tangent plane to 
with the lobe pattern of
Fig. 5.
At the equator ( 
),
the lobes are oriented 
from the line of sight
and rotate into and out of the tangent plane with 
.
The polarization pattern here is a pure U-field which varies
in magnitude as 
.
At the pole 
, there are no temperature variations in the
tangent plane so the polarization vanishes.
Other angles can equally well be visualized by viewing the
quadrupole pattern at different orientations given by .
The full 
, m=1 pattern,
is displayed explicitly in Fig. 6 (yellow lines, real part). Note that the pattern is dominated by U-contributions especially near the equator. The similarities and differences with the scalar pattern will be discussed more fully in §3.
