Temperature fluctuations in the CMB arise due to the variations
in the matter density. After last-scattering CMB photons
stream freely to us and the temperature fluctuations are
seen as CMB temperature differences (anisotropy)
across the sky. Anisotropy on a given angular scale is related
to density perturbations with wavelengths corresponding to
the length projected by that angle on the last-scattering surface:
![]() . Until the ions and
electrons ``recombined'' at last-scattering, the photons and ions and
electrons (the baryons) were tightly coupled by Thomson scattering,
and behaved as a single fluid. The gravity-driven collapse of a
perturbation is resisted by the pressure restoring
force of the photons. Fourier mode k of the temperature
fluctuation is governed by a harmonic-oscillator like equation,
. Until the ions and
electrons ``recombined'' at last-scattering, the photons and ions and
electrons (the baryons) were tightly coupled by Thomson scattering,
and behaved as a single fluid. The gravity-driven collapse of a
perturbation is resisted by the pressure restoring
force of the photons. Fourier mode k of the temperature
fluctuation is governed by a harmonic-oscillator like equation,
where F is the gravitational forcing term due to the dark matter,
![]() describes the inertia of the fluid,
and primes denote derivatives with respect to (conformal) time
(
describes the inertia of the fluid,
and primes denote derivatives with respect to (conformal) time
( ![]() ). The solutions are acoustic waves.
). The solutions are acoustic waves.
The large-angular scale (Sachs-Wolfe) plateau ( ![]() )
in the angular power spectrum arises from
perturbations with periods longer than the age of the Universe at
last scattering. CMB photons lose energy climbing out of the
potential wells associated with these long-wavelength density
perturbations, and the temperature differences seen on the sky reflect
the gravitational potential differences on the last-scattering surface.
If the density fluctuations are approximately scale-invariant, as inflation
and defect theories predict, the plateau in the angular power spectrum is flat.
)
in the angular power spectrum arises from
perturbations with periods longer than the age of the Universe at
last scattering. CMB photons lose energy climbing out of the
potential wells associated with these long-wavelength density
perturbations, and the temperature differences seen on the sky reflect
the gravitational potential differences on the last-scattering surface.
If the density fluctuations are approximately scale-invariant, as inflation
and defect theories predict, the plateau in the angular power spectrum is flat.
The baryon - photon fluctuations that produce anisotropy on sub-degree
angular scales ( ![]() ) have sufficient time to undergo oscillation.
At maximum compression (rarefaction) the CMB temperature is higher (lower)
than average; neutral compression corresponds to velocity maximum of the
fluid, which leads to a Doppler-shifted CMB temperature.
Since last-scattering is nearly instantaneous the CMB provides a snapshot of
these acoustic oscillations, with different wavelength modes being caught
in different phases of oscillation. Because a given multipole
) have sufficient time to undergo oscillation.
At maximum compression (rarefaction) the CMB temperature is higher (lower)
than average; neutral compression corresponds to velocity maximum of the
fluid, which leads to a Doppler-shifted CMB temperature.
Since last-scattering is nearly instantaneous the CMB provides a snapshot of
these acoustic oscillations, with different wavelength modes being caught
in different phases of oscillation. Because a given multipole ![]() is
dominated by the effects of a narrow band of Fourier modes
(
is
dominated by the effects of a narrow band of Fourier modes
( ![]() ), this leads to peaks and valleys in the angular power
spectrum. The peaks are modes which were maximally under- or overdense at
last-scattering, and the troughs are velocity maxima, which are
), this leads to peaks and valleys in the angular power
spectrum. The peaks are modes which were maximally under- or overdense at
last-scattering, and the troughs are velocity maxima, which are ![]() out
of phase with the density maxima.
out
of phase with the density maxima.
On the smallest scales ( ![]() ) the spectrum is exponentially
damped, due to the finite thickness of the last-scattering
surface. Features on these angular scales are washed out because
last scattering is not a single snapshot,
but a montage of snapshots which blurs the fine details.
) the spectrum is exponentially
damped, due to the finite thickness of the last-scattering
surface. Features on these angular scales are washed out because
last scattering is not a single snapshot,
but a montage of snapshots which blurs the fine details.
The precise shape of the power spectrum depends upon cosmological
parameters as well as the underlying density perturbations and thereby
encodes a wealth of information; see Fig.6.
The position of the first peak is sensitive to the total energy density
and can be used to determine the geometry of the Universe:
Other features encode other information. For example,
the height of the first peak depends
upon the matter and baryon density (which both depend on the Hubble constant)
and the presence of a cosmological constant.
If the spectrum of density perturbations is not scale invariant,
but for example has more power on small scales, the angular power
spectrum rises with increasing
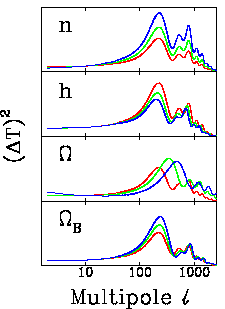 Fig.6: The dependence of the angular power spectrum upon some of the
cosmological and model parameters. In each panel the red curve is CDM
with
Fig.6: The dependence of the angular power spectrum upon some of the
cosmological and model parameters. In each panel the red curve is CDM
with ![]() ,
, ![]() , n=1 and h=0.5; the other curves
show the effect of varying these parameters one at a time, with the
parameter increasing (decreasing for
, n=1 and h=0.5; the other curves
show the effect of varying these parameters one at a time, with the
parameter increasing (decreasing for ![]() ) from red through green
to blue.
) from red through green
to blue.
![]() .
It moves to smaller angles as
.
It moves to smaller angles as ![]() decreases because the distance to the
last-scattering surface increases (the expansion slows less in a low-density
universe) and geodesics diverge in negatively curve space (fixed distance on
the last-scattering surface subtends a smaller angle).
decreases because the distance to the
last-scattering surface increases (the expansion slows less in a low-density
universe) and geodesics diverge in negatively curve space (fixed distance on
the last-scattering surface subtends a smaller angle).
![]() .
.
![]()
![]()
![]()
Next: About this document
Up: The Science Harvest: From
Previous: Box 1: Big-bang Basics