The COBE DMR detection of temperature fluctuations of amplitude
![]() K on the
K on the ![]() provided the first evidence for the density
inhomogeneities from which all structure in the Universe is believed to
have originated.
The level of inhomogeneity is consistent with that needed to account for
the structure seen today through the attractive action of gravity over the
past 13 billion years. For theories like inflation and topological defects,
which specify the shape of the spectrum of inhomogeneity, the accurate (10%)
DMR measurement allows extrapolation from COBE scales, 1000's of
Mpc, to the length scales relevant for the formation of galaxies, clusters of
galaxies, and other structures seen today, leading to more precise predictions
about the development of structure. Overnight, the term
``COBE
normalized'' became a part of the cosmological vernacular.
provided the first evidence for the density
inhomogeneities from which all structure in the Universe is believed to
have originated.
The level of inhomogeneity is consistent with that needed to account for
the structure seen today through the attractive action of gravity over the
past 13 billion years. For theories like inflation and topological defects,
which specify the shape of the spectrum of inhomogeneity, the accurate (10%)
DMR measurement allows extrapolation from COBE scales, 1000's of
Mpc, to the length scales relevant for the formation of galaxies, clusters of
galaxies, and other structures seen today, leading to more precise predictions
about the development of structure. Overnight, the term
``COBE
normalized'' became a part of the cosmological vernacular.
In the five years since the COBE DMR detection, anisotropy on angular
scales from ![]() to
to ![]() has been detected by about twenty
different experiments.
Because these experiments have had to deal with the effect of the atmosphere,
limited sky coverage and calibration difficulties, they have been less precise
than COBE.
These experiments have not resolved individual multipoles, but rather
``broad-band power'' in multipole intervals
has been detected by about twenty
different experiments.
Because these experiments have had to deal with the effect of the atmosphere,
limited sky coverage and calibration difficulties, they have been less precise
than COBE.
These experiments have not resolved individual multipoles, but rather
``broad-band power'' in multipole intervals ![]() .
Nevertheless, they have added much to our understanding
and a picture is emerging: A rise in the level of anisotropy on degree
scales and an apparent drop at smaller angular scales
(see Fig.2).
This is consistent with the first acoustic peak.
Together with COBE, these experiments now cover almost three decades
in angular scale; they are generally consistent with inflation, have eliminated
all models of structure formation that do not incorporate nonbaryonic
dark matter,
and disfavor topological-defect models.
.
Nevertheless, they have added much to our understanding
and a picture is emerging: A rise in the level of anisotropy on degree
scales and an apparent drop at smaller angular scales
(see Fig.2).
This is consistent with the first acoustic peak.
Together with COBE, these experiments now cover almost three decades
in angular scale; they are generally consistent with inflation, have eliminated
all models of structure formation that do not incorporate nonbaryonic
dark matter,
and disfavor topological-defect models.
Much will happen before MAP and Planck.
A new generation of experiments, instruments flown on long-duration
balloons or located on high-dry sites like the South Pole or Atacama
in Chile, should begin to define the prominent acoustic peaks in the
multipole spectrum by measuring
power in multipole windows
![]() from
from ![]() to
to ![]() .
(Resolution in
.
(Resolution in ![]() is increased by covering more sky, since
is increased by covering more sky, since ![]() and
and
![]() are ``Fourier'' conjugate variables.)
By resolving the position of the first two or three peaks, these experiments
should be able to pin down the density parameter
are ``Fourier'' conjugate variables.)
By resolving the position of the first two or three peaks, these experiments
should be able to pin down the density parameter ![]() to an accuracy of
20% and in so doing test the inflationary prediction of a flat Universe.
They should also begin to determine other cosmological
parameters, e.g., the baryon density and the Hubble constant, to a precision
of 200r so.
to an accuracy of
20% and in so doing test the inflationary prediction of a flat Universe.
They should also begin to determine other cosmological
parameters, e.g., the baryon density and the Hubble constant, to a precision
of 200r so.
Using low-frequency receivers (22-90GHz), MAP will determine
the angular power spectrum out to ![]() to a precision nearly
limited by sampling variance.
Planck is expected to reach
to a precision nearly
limited by sampling variance.
Planck is expected to reach ![]() with a similar precision,
and should have better discrimination against foreground sources by virtue of
both high and low frequency coverage.
Together, they should come close to reaping almost all the information
encoded in CMB temperature anisotropy (see Fig.4).
with a similar precision,
and should have better discrimination against foreground sources by virtue of
both high and low frequency coverage.
Together, they should come close to reaping almost all the information
encoded in CMB temperature anisotropy (see Fig.4).
Many of the cosmological parameters, including the density parameter
The CMB
anisotropy should be polarized
at the level of around 5%, and both
MAP and Planck will have the capability of detecting it.
The polarization arises because Thomson scattering is partially polarized
(depending upon the scattering angle) and the CMB radiation field
is not isotropic before last-scattering due to the temperature
fluctuations induced by density perturbations.
Polarization, which has yet to be detected, provides a consistency check on
the basic picture of anisotropy formation and has the potential to improve
the accuracy with which cosmological parameters can be determined.
It is likely that there will still be much to learn from CMB polarization
after MAP and Planck.
In particular, polarization might be very useful in separating the
contribution of inflation-produced gravity waves to CMB anisotropy, as
gravity waves induce a different pattern of polarization than density
perturbations do. Determining the level of gravitational
radiation fixes the energy scale of inflation.
Polarization is also crucial for detecting the re-ionization of the neutral
transparent Universe by the first generation of stars or quasars. These
objects are thought to have appeared at redshifts of around ten to twenty,
and ended the ``dark age'' that began with last scattering.
Beyond its immense value as a cosmic Rosetta stone, the CMB is being used
for other purposes. Perhaps the most exciting is ``microwave tomography''
of clusters of galaxies using the S-Z effect.
In 1972 Sunyaev and Zel'dovich pointed out that some of the
CMB photons passing through the hot gas in clusters are scattered to higher
energy by inverse Compton scattering (S-Z effect). This leads to a small
spectral distortion of the CMB whose amplitude depends on the temperature
and density of the cluster gas, but is independent of redshift. The S-Z
effect can be used to the study the structure of clusters as well as to
search for clusters at high redshift where the galaxies may be too faint
to be seen, or may not even be present. Further,
by comparing S-Z maps with x-ray maps of clusters
(see Fig.5),
the Hubble constant can be determined without recourse to
the usual method of ``standard candles.''
That's because the S-Z distortion is proportional to the line-of-sight
integral of the electron density whereas the X-ray intensity is proportional
To the integral of the square. Comparing the two yields a determination
of the clusters size.
The Cosmic Microwave Background has played a central role in cosmology
since its discovery in 1965. It is one of the cornerstones of
the standard hot big-bang theory. The study of CMB anisotropy with
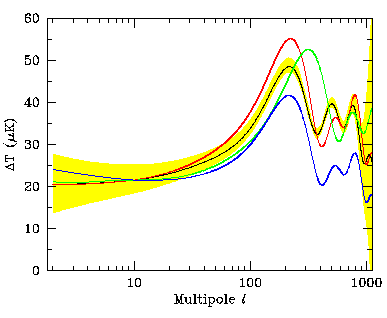 FIG.4
NASAs MAP satellite which will fly in the year 2000, should easily
be able to discriminate between variants of cold-dark matter cosmology:
The favored critical density universe to which baryons contribute 5% (black
curve with yellow band)
or 10% (red); an open universe with
FIG.4
NASAs MAP satellite which will fly in the year 2000, should easily
be able to discriminate between variants of cold-dark matter cosmology:
The favored critical density universe to which baryons contribute 5% (black
curve with yellow band)
or 10% (red); an open universe with ![]() (green);
and ``tilted'' CDM with n=0.8 (blue).
The expected one sigma-error per multipole for MAP
is indicated by the thickness of the yellow band (the band blows up at large
(green);
and ``tilted'' CDM with n=0.8 (blue).
The expected one sigma-error per multipole for MAP
is indicated by the thickness of the yellow band (the band blows up at large
![]() because the
because the ![]() beam smears out smaller features).
beam smears out smaller features).
![]() ,
can be determined from the CMB
without reference to a
specific theory.
However the true power comes from detailed modelling within a given
theoretical framework.
For a theory like inflation + cold dark matter the theoretical angular power
spectrum depends upon ten or so parameters, including
,
can be determined from the CMB
without reference to a
specific theory.
However the true power comes from detailed modelling within a given
theoretical framework.
For a theory like inflation + cold dark matter the theoretical angular power
spectrum depends upon ten or so parameters, including ![]() ,
, ![]() , the
power-law index n that characterizes the spectrum of density perturbations
(n=1 corresponds to scale invariant perturbations), the composition of the
dark matter (fraction of critical density in cold dark matter, light neutrinos,
and cosmological constant), the amount of gravitational radiation produced
during inflation, and a few others.
These parameters are very overconstrained by the 2500 multipoles that will be
measured, so that the theory can be thoroughly tested. Furthermore
the Hubble constant, baryon density, mass density and spectral index
will all be determined to within a few percent.
, the
power-law index n that characterizes the spectrum of density perturbations
(n=1 corresponds to scale invariant perturbations), the composition of the
dark matter (fraction of critical density in cold dark matter, light neutrinos,
and cosmological constant), the amount of gravitational radiation produced
during inflation, and a few others.
These parameters are very overconstrained by the 2500 multipoles that will be
measured, so that the theory can be thoroughly tested. Furthermore
the Hubble constant, baryon density, mass density and spectral index
will all be determined to within a few percent.
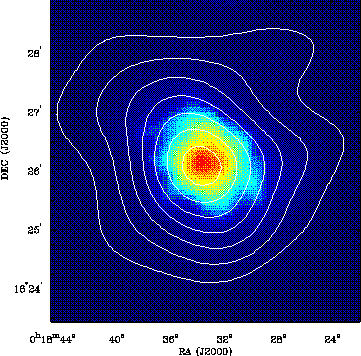
FIG.5
Comparing microwave tomography (contour lines) of a galaxy cluster (CL0016+16)
with an X-ray image of its hot intergalactic gas (false colors) provides a
way of measuring the Hubble constant without standard candles.
Figure courtesy of John Carlstrom and Marshall Joy.
![]() K precision and fraction of a degree angular resolution is likely to
have as least as much impact as the discovery of the CMB.
It will put to the test our most promising ideas about the earliest moments
and will determine for us the elusive fundamental parameters of cosmology.
K precision and fraction of a degree angular resolution is likely to
have as least as much impact as the discovery of the CMB.
It will put to the test our most promising ideas about the earliest moments
and will determine for us the elusive fundamental parameters of cosmology.
![]()
![]()
![]()
Next: Box 1: Big-bang Basics
Up: Rosetta Stone
Previous: Mapping to MicroKelvin Precision
Sun Nov 2 13:44:30 CST 1997