THE IFIRS FAQ
SUMMARY
The goal of IFIRS is to
obtain ultra-deep, wide field, diffraction limited, imagery from near-
to mid-IR wavelengths, with flexible spectral resolution. IFIRS is a
Michelson interferometer
configured as an imaging Fourier
transform spectrometer (IFTS).
IFIRS is a high throughput, wide field, diffraction-limted imager.
Since IFIRS is an FTS, it is both a camera and a multi-object
or integral field
spectrometer. As a camera IFIRS has unusual flexibility of
spectral resolution, and a unique pan-chromatic imaging mode.
SPECIAL FEATURES
Currently three spectrometer architectures viable for NGST: tunable filter
(e.g., Fabry Perot), dispersive (e.g, a MOS or IFU), and Fourier transform.
There is no single correct answer, because each concept has strengths and
weaknesses, and is best in a particular domain. The correct choice depends
on the type of the observations demanded by the science, detector performance,
and the nature of the backgrounds.
The signal-to-noise
performance of 3-d imaging spectrometers equipped with 2-d detector
arrays is the same for all architectures, in the ideal case of photon shot
noise limted operation. This is correct so long as the spectrometers
are equipped with the same size arrays, and the same spatial and spectral
degrees of freedom of the astronomical scene are observed.
Specific advantages of the IFTS are:
-
Slitless multi-object spectrometer and camera
-
Spectrum for every pixel
-
Hands-off/unbiased object selection
-
Efficient in the confusion limit
-
Works for moving objects
-
Variable resolution
-
Continuously adjustable from R=1-10,000
-
High throughput
-
~ 80%, including detector QE, optics, & beam splitter
-
Large free spectral range ( ~ 3 octaves)
-
Instantaneous broad wavelength coverage
-
High SNR pan-chromatic imaging (for science and guiding)
-
Tolerant of cosmic rays, detector
noise, and light leaks
-
Precision calibration
-
Accurate spectrophotometric calibration
-
Absolute wavelength scale and precisely defined wavelength response
-
High SNR determination of flat-fields & detector non-linearity
Deep imaging is acquired simultaneously with higher spectral resolution
data over a broad wavelength range. IFIRS has a pan-chromatic mode
that is peculiar to a four port interferometer. The summed signal from
the two output ports is unmodulated and corresponds to the total broad-band
photon flux entering the instrument. With a simple camera a pan-chromatic
image can be formed with by summing individual filter images . The IFTS
pan-chromatic image has a speed
advantage factor that is equal to the number of filters used.
IFIRS also has a hybrid, or dispersed FTS mode. In a regular FTS, spectral
information is encoded in the z-direction of the data cube, and there is
no mixing of spectral and spatial information. The advantage is that a
spectrum is recorded for every pixel on the sky. The penalty is that the
photon shot-noise from all spectral channels is present at each frequency.
This shot-noise can be reduced by masking the telescope focal plane around
objects of interest with a programmable micro-mirror array, and inserting
a prism into the collimated space. The dispersed FTS mode is used
to obtain the highest possible sensitivity at high spectral resolution
(R=600-10,000). The slit width does not determine the spectral resolution
in the dispersed FTS mode, since the spectral resolution is derived from
the interferograms. The dispersed FTS data-cube contains spectra which
are tilted with respect to the z-axis. The tilt angle is the arc tangent
of the ratio of spectral resolutions of the dispersive element and interferometer.
The dispersed FTS has better SNR performance than the pure FTS, and the
source density of object slits is higher than for the pure multi-object
spectrometer.
DESIGN
On the object side, a collimator illuminates the interferometer with parallel
light. The interfering beams are collected by a camera, creating a one-to-one
mapping between points in the object and image planes. By placing
a detector focal plane array at the focus of the camera, each pixel is
matched to a single point on the sky. At any given optical path difference
(OPD) the image of the sky is modulated spatially by the interferometer
fringe
pattern, which encodes the spectral information. By recording
images of the sky at different OPDs, the spectrum of each pixel can be
reconstructed. The OPD is scanned in discrete steps since FPAs are integrating
detectors. Scanning the OPD in this fashion generates a data cube.
The set of signals from the pixels in each frame corresponding to a particular
point in the sky forms an independent interferogram. These interferograms
are Fourier transformed individually yielding a spectral data cube composed
of the same spatial elements as the image. The sampling theorem establishes
the number and amplitude of OPD steps necessary to recover the spectrum
at a given resolution.
The major components of IFIRS are the collimator, interferometer, cameras,
and focal plane arrays and associated electronics. Two important
ancillary subsystems are the metrology system and the calibration unit.
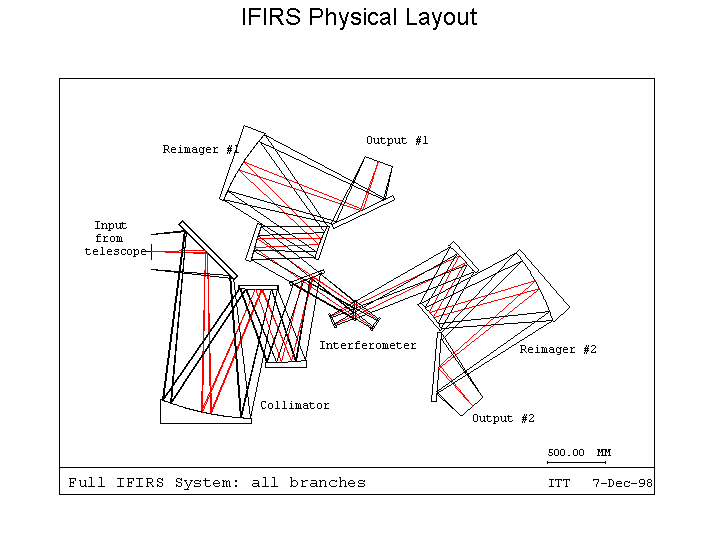 (Note: For simplicity only the near-IR FPA arrays have been shown
at the output ports. The final fold mirror is either a dichroic
or flip-mirror which directs the mid-IR light to the mid-IR detectors).
(Note: For simplicity only the near-IR FPA arrays have been shown
at the output ports. The final fold mirror is either a dichroic
or flip-mirror which directs the mid-IR light to the mid-IR detectors).
The collimator is a three mirror anastigmat (TMA) which illuminates a four-port
Michelson. There are two input and two output ports. One input port
is fed with the sky signal, the other input can be illuminated by the calibration
unit. The interferometer consists of a 50:50 reflecting/transmitting
beam
splitter, and two cube-corner retroreflectors. The appropriate
beam splitter is selected using a filter-wheel mechanism. One cube-corner
is located on a translation stage, which permits precision control of the
OPD. The OPD is monitored using a laser diode interferometric metrology
system. Each output port of the interferometer feeds identical TMA cameras.
A final reflection (an articulated fold mirror or a static dichroic) directs
short wavelength radiation to the near-IR FPA and long wavelength radiation
to the mid-IR FPA.
What spectroscopic resolution(s)
are available?
The spectral resolution of an IFTS is determined by the maximum optical
path difference at which the interferogram is measured, and hence is continuously
variable. IFIRS can obtain pan-chromatic imagery (R ~ 1), broad-band photometry
(R ~ 10), low resolution spectrophotometry (R ~ 100), diagnostic spectroscopy
(R ~ 1000) and kinematics (R ~ 10,000).
The optical path difference can be scanned from 0-0.5 cm, hence the
maximum spectral resolution is 30 GHz (1 wavenumber). The spectral resolution
is fixed in frequency, so the maximum resolution is 10,000 at 1 µm
and 1000 at 10 µm.
What wavelength coverage/simultaneous
wavelength coverage is available?
All the optical components, apart from the detectors and beam splitter,
are based on reflective optics, and potentially support a very broad spectral
range, from near UV to far-IR.
IFIRS has two detector channels: near-IR (InSb
0.6-5.6
µm) and mid-IR (HgCdTe
3-15 µm). Operation is optimized for one channel by selection
of the appropriate beam splitter. Beam
splitters typically span a free spectral range of x6 in wavelength,
and the entire band pass is observed simultaneously. There are three
high-efficiency beam splitters which span 0.6-3.4 µm, 0.96-5.4
µm, and 2-21
µm.
The long wavelength cut-off of the HgCdTe array is to be determined;
11 µm is currently feasible, operation as long as 15 µm should
be anticipated, and17 µm may be possible. These detectors can
operate at the ISIM operating temperature of 30 K without additional cooling.
IFIRS can tolerate the relatively high dark current of HgCdTe since it
integrates the entire mid-IR band on the detector and operates in a background
noise limited regime. Should space qualified cryocoolers be made
available, then Si:As BIB arrays will be used instead to extend the wavelength
coverage to 28 µm.
In the current design, we have optimized the operation for a single
channel, and simultaneous near- and mid-IR observations are not supported.
Replacement of the final fold-mirror with a dichroic would introduce some
losses (~ 10%), and eliminate two mechanisms. Using the long wavelength
beam splitter and both detectors would yield simultaneous 2-15 micron observations
with good efficiency.
What is the instrument's spatial resolution?
The spatial resolution of IFIRS is determined by the combined performance
of the telescope and instrument optics. This yields:
-
150 nm rms wave front error
-
Strehl ratio of 0.8 at 2 µm
-
IFIRS is diffraction limited at 2 µm with a FWHM ~ 0.052" for an
8m primary.
The IFIRS wave front error budget includes:
-
Design residuals
-
Fabrication errors
-
Alignment tolerances
-
Interferometer optics
-
Mechanical & thermal deformation
The pixel sampling is:
-
Near-IR channel pixel size is 0."0386 - Nyquist sampled at 3 µm
-
Mid-IR channel pixel size is 0."0772 - Nyquist sampled at 6 µm.
The choice of pixel scale is not final. Since diffraction limited images
can be constructed from a set of dithered images we will probably choose
to be undersampled. Lauer (PASP, 111, 227) has
shown that the reconstructed image is an exact representation of the data
set with no loss of resolution at the Nyquist scale. Undersampling is advantageous
for projects that require large instantaneous field of view, e.g., supernova
cosmology.
What is the instrument's field of view?
The current optical design of IFIRS provides a corrected field of 5.'28
x 5.'28 (317" x 317"). This is designed to illuminate a 8192 x 8192 near-IR
focal plane array. The mid-IR field of view is limited by the focal plane
array (2048 x 2048) and is 2.'64 x 2.'64.
What is the minimum object spacing for multiobject
observations?
The IFTS is a true integral field spectrometer. There are no slits. There
is a spectrum for every pixel in the field of view. The near-IR focal plane
is Nyquist sampled at 3 µm. With appropriate drizzling, spatial information
can be recovered down to the diffraction limit. Thus we expect minimum
object spacing to be of the order of the size of the Airy disk (FWHM =
0."05) at 2 µm. 3-d PSF fitting ("3-d DAOPHOT") should be able to
successfully extract spectra on these scales.
In simulated data of crowded fields we have
successfully used optimal extraction using a 3-d kernel which has width
equal to the PSF.
In many cases source crowding may be the limiting factor, e.g., in studies
of stellar populations in nearby galaxies. With IFIRS, unambiguous spectral
extraction can be performed down to the confusion limit.
The dispersed FTS mode is used to obtain the highest possible sensitivity
at high spectral resolution (R=600-10,000),
Assuming that a micro-mirror array is available, a great deal of flexibility
in terms of object selection may be had. The viewed portion of the image
may be arranged so that the "objective prism streaks" from each target
do not overlap. In the baseline concept, a prism disperses the 0.6-5 micron
spectral range over approximately 500 pixels. Thus any number of objects
that were separated in the field of view in a direction orthogonal to the
dispersion direction, can be simultaneously observed. In the dispersion
direction, a separation of 500 pixels, (19") is required for the near-IR
channel to avoid overlap.
What is the number of objects that can be
observed simultaneously?
In the near-IR channel the FPA is 8192 x 8192. If we conservatively assume
that an 8x8 subarray is needed to record one object, then we can record
spectra for a million objects. The mid-IR channel has 16 times fewer pixels,
and therefore correspondingly fewer spectra.
With an image mask the number of obects which can be observed simultaneously
is reduced to ~ 17,000.
What is the speed of setup?
The instrument specific setup to begin an IFIRS observation consists of:
-
Pure FTS mode
-
Select beam splitter
-
Command optical path difference
-
Dispersed FTS mode
-
Select beam splitter
-
Command optical path difference
-
Select prism
-
Configure focal plane mask (micro-mirror array)
The major mechanisms (beam splitter & prism) take < 100 s to select.
The time to acquire and stabilize a given optical path difference is <
2 s.
Precise absolute pointing is not required for the pure FTS mode ---
only accurate tracking during a single exposure (t = 100-1000 s) is needed.
What is the expected instrument throughput as
a function of wavelength?
The throughput of the FTS is limited by the reflectivity of metal optics,
beam splitter efficiency, and detector QE. There are no slit losses or
light scattered by gratings in pure FTS mode.
There are 12 gold reflections
(~ 99% per surface) - input fold mirror, TMA collimator, fold mirror, three
reflections at a cube corner, final fold mirror, and a TMA camera.
We have detailed designs for optimized
0.96-5.4 & 2-21 micron beam splitters.
The resultant average in-band throughputs are 86% and 87% respectively
for the near- and mid-IR. The in-band response is flat. If we include
detector
QE, the total
system efficiency is 75% (InSb), and 63% (HgCdTe).
We have not designed a 0.6-3.4 micron beam splitter, but the average
throughput will be ~ 80%. Gold is not optimal for 0.6-0.8 µm, and
the efficiency in this range is reduced by 12%. An alternative coating,
e.g., protected silver, would recover the 0.6-0.8 micron performance at
the expense of a serveral percent loss at longer wavelengths.
What are the calibration requirements?
A four port Michelson interferometer is intrinsically a superb instrument
from a calibration point of view. The measured interferogram results
from the difference between spectra of sources at the two input ports.
Calibration sources placed at the second input port act as transfer standards
for full radiometric calibrations performed on the ground prior to flight.
The mid-IR channel is calibrated by varying the temperature of a cold blackbody
at the second input that fills the field of view. The near-IR channel
is calibrated using a dilute, hot blackbody, that does not produce excessive
heating of the instrument. In both cases, a full calibration of each FPA
pixel's offset, spectral responsivity, and non-linearity can be conducted
by varying integration times or source intensities and collecting data
in the normal manner. This capability is invaluable should the system
response change due to exposure to the space environment.
The telescope and relay optics are not calibrated using the internal
source, but inferred by observation of standard stars. On orbit,
observations of standard stars will be used to cross-calibrate the on-board
sources. Periodic observations of the same reference stars will then
be used to monitor performance.
The absolute wavelength calibration is provided by the interferometer
metrology system, which is reference to a diode laser. The accuracy
should be better than 7.5 GHz (0.25 wavenumbers). This provides the
wavelength calibration for both pure and dispersed FTS modes.
What telescope performance (e.g. pointing and tracking,
image quality) is required?
The telescope and instrument should contribute equally to the overall system
wave front error budget. The pointing stability should therefore be approximately
0."003 pixel (3 sigma). This stability need only be maintained no
longer than a typical integration time (1000 s for the near-IR, 100 s for
mid-IR).
Carefully controlled dithering of the line of sight, accurate to 0".003
with an amplitude of about 1", should be required to extract diffraction
limited spatial information from undersampled images, to veto cosmic ray
contaminated pixels, and to replace data from dead pixels. Significant
image motion between subsequent frames of the interferogram does not degrade
spectral or spatial resolution. In particular, the FTS can obtain spectra
of moving objects such as solar system targets.
What is the general tradeoff between the instrument's
spectral resolution and coverage vs. spatial resolution/distribution?
An important trade is between band-pass and sensitivity. The FTS works
broad-band, so the in-band photon shot-noise is associated with every spectral
channel. A blocking filter reduces the spectral coverage and increases
the SNR. For a flat photon spectrum, and shot-noise limited operation,
reducing the number of spectral channels increases the SNR in each spectral
channel by the square root of the bandwidth reduction factor. The SNR in
the pan-chromatic image is reduced by the square root of this factor, since
less light is being collected. Simulations suggest that for many
DRM programs the scientific value of more spectral channels outweighs the
associated decrease in SNR (e.g., measuring photometric redshifts) , and
that a likely workhorse operating point would be for R ~ 100.
When higher spectral resolution (R=600-10,000) observations of high
latitude "blank fields" are required (e.g., for the galaxy evolution DRM),
there are too few bright objects to warrant the full spatial multiplex
advantage of the IFTS. In this case the dispersed-FTS option gives
the ultimate sensitivity at the expense of reduced number of targets (see
5 & 6).
What observing modes are expected to exist?
What are your priorities for instrument modes?
-
PURE FTS MODE (1st priority)
In this mode the instrument functions as a camera with tuneable filters.
A menu of OPD scans will be provided yielding different resolutions (R
= 1, 2, 4, 8, ...) or number of spectral channels, and integration time
apodization (top hat, Gaussian, etc.). The combination of these options
can be used to synthesize band-passes with different widths and profiles
and ranging from broad-band filters (R ~ 5), e.g., RIJHKLM etc., to narrow
band imaging (R ~ 300).
In this mode the major instrument configuration option is the choice
of beam splitter. Observations in mid-IR will be obtained by exchanging
the beam splitter, and acquiring data with the HgCdTe focal plane array.
As stated above, in certain cases simultaneous near- and mid-IR observations
are possible.
-
DISPERSED FTS MODE (2nd Priority)
This mode is a hybrid mode for higher spectral resolution (R=600-10,000)
observations of sparsely distributed objects. A mask is placed in
an upstream image plane, centered around the object or objects of interest,
(e.g., a programmable micro-mirror array) and a prism is inserted into
the collimated space.
-
SLITLESS PRISM MODE (3rd Priority)
This is an objective prism mode for resolutions from R=5-500 for densely
distributed, but not space filling, objects, such as Galactic star clusters.
There is no slit in the upstream image plane, but the dispersing prism
is in place in collimated space. If the dispersed FTS mode is implemented,
then this mode comes for free.
All of the above modes are compatible with a coronographic "hole" in
the upstream image plane.
What do you expect are the major issues
on observing strategy (e.g. acquisition images, object selection)?
Because a spectrum is obtained for every pixel, it is not necessary to
define the region of any given object to be fed to a spectrometer before
the data is acquired, and indeed, after the fact, a spatially extended
set of spectra can be averaged in a weighted sum tailored to maximize the
sensitivity for detection of any particular feature of interest.
The major issue is simply the decision as to the mode to use from the three
described in the answer to question (12), the desired spectral channel
and bandpass, the spectral resolution, and the observing time.
How will the instrument performance depend on
the on-orbit performance of the detectors (e.g. cosmic ray susceptibility)?
By virtue of being able to acquire spectra with the full bandpass of light
impinging on the detector elements, an FTS is tolerant of detector performance
degradation, both in terms of dark current and read noise. Furthermore,
by taking a series of readouts to effectively monitor the apparent photo-current,
large cosmic ray glitches can be removed on orbit. Also, because spectral
information is derived from modulated light levels, the 1/f type of focal
plane array glitch noise which is apparently very significant for instruments
such as those on ISO, can be very significantly reduced. Using the observed
ISO cosmic ray glitches as an example, the suppression of
glitch noise by IFIRS could reasonably be expected to exceed an order
of magnitude.
Are there any major technical challenges
to be faced?
-
Beam splitters
-
Large (8-12 cm) elements are needed
-
High surface quality (lambda/20) is necessary to preserve image quality
and modulation efficiency
-
Robust material are essential to survive launch
-
Thermal management
-
The power budget for the ISIM is extremely restrictive
-
The power dissipation and parasitic losses of the 8k x 8k focal plane arrays
are a concern
-
Data rates
-
The near-IR channel of IFIRS can produce about 11 Gb/day (uncompressed).
-
Mid-IR performance
-
Operation longer than 11 µm either needs development of low dark
current HgCdTe or 8K closed cycle cooler to permit operation of Si:As BIBs.
Back to the Berkeley NGST page.


